Geometric Shapes: Ellipses
An ellipse is a perfect circle that has been foreshortened. Ellipses are used to construct cylinders and cones.
The following sections will examine the parts of an ellipse and how to draw ellipses in perspective.
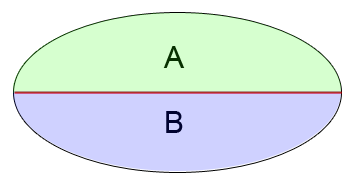
Ellipse Areas: In an ellipse, the area of half A will always be equal to the area of half B.

Ellipse Areas: Even when the ellipse changes size, half A will always have the same area as half B.
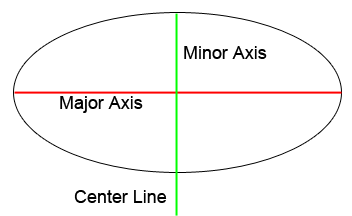
Review of an ellipse: The major axis extends from the two longest parts of the ellipse. The minor axis extends from the two shortest parts of the ellipse. The center line of an ellipse will always have the same direction and placement as the minor axis and extends beyond the ellipse.
To draw an ellipse:
1. Determine the size by lightly drawing the major axis.
2. Find the exact center of the major axis line and draw another line perpendicular to the major axis with the distance above the major axis being equal to the distance below the axis. This is your minor axis and this will determine the pitch of the ellipse.
3. Gently draw the curved ends on the major axis. When both curves are symmetrical, lightly draw in the remaining portion of the ellipse above and below the major axis, making sure that the curves touch the top and bottom of the minor axis line. The division of the axis lines will create four equal-mirrored quadrants.
4. Check and correct for symmetry, and draw finished, darker lines.
Ellipses contained within squares
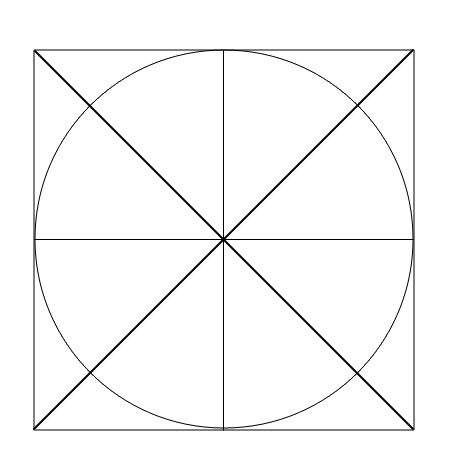
Center of Ellipse: In this example, starting with a square, the exact center was determined by drawing diagonal lines from corner to corner. Extending vertical and horizontal lines from the center to the outside edges created four equal quadrants. A circle placed inside the square would touch the ends of the vertical and horizontal lines.
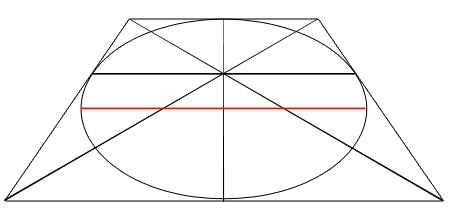
Center of Foreshortened Circle: When the square/circle is foreshortened, the top half of the circle is smaller than the bottom half because of diminution. The vertical line remains as the minor axis, but the horizontal line indicating the perspective center of the square is not the major axis. The red line represents the major axis, and is the measureable center between the top and bottom curves of the ellipse. Click the thumbnails below to compare the top and bottom half of the ellipse with its correct major axis placement.
Perspective Center vs. Major Axis: Notice that the red major axis line does not pass through the perspective center of the foreshortened circle and does not touch the edge of the foreshortened square. The major axis will always be at the widest point of the ellipse, with the top half equal to the bottom half.
Within an ellipse, the top half and the bottom half are always identical. The major axis is the widest point of the ellipse. It will be located at the exact center of the minor axis.


Ellipses on a beach ball: Notice that even though a beach ball has six different colored segments, they are created with just three ellipses. Each ellipse has its own major and minor axis.
Note: The line on this beach ball connects the rotated top and bottom of the ball. It is not the center line of any of the ellipses.
Errors with ellipses
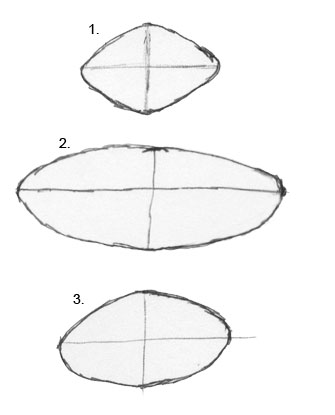
When drawing ellipses, the lines should appear to wrap around the object by having rounded ends.
A common drawing problem is to draw ellipses like “footballs,” having pointed corners. Pointed ends give the illusion of a creased circle. Remember, ellipses are perfect circles foreshortened in perspective.
Another common problem is to have unequal distances of the axis above and below the major axis, which results in a different pitch above and below the major axis.