The Aggregate Expenditures Model
Section 01: The Aggregate Expenditures Model
Now we will build on your understanding of Consumption and Investment to form what is called the Aggregate Expenditures Model. This model is used as a framework for determining equilibrium output, or GDP, in the economy. When we developed the Consumption Function in a previous lesson, we stated that Consumption was a function of Disposable Income. In this model, we return to the assumption of the Circular Flow Model that the production of the final goods and services in the economy (the GDP) results in a flow of income that is exactly equal to the value of that output. Since the GDP is equal to Income, we can model the Spending (for now just Consumption and Investment) in the economy in terms of GDP instead of in terms of Income.
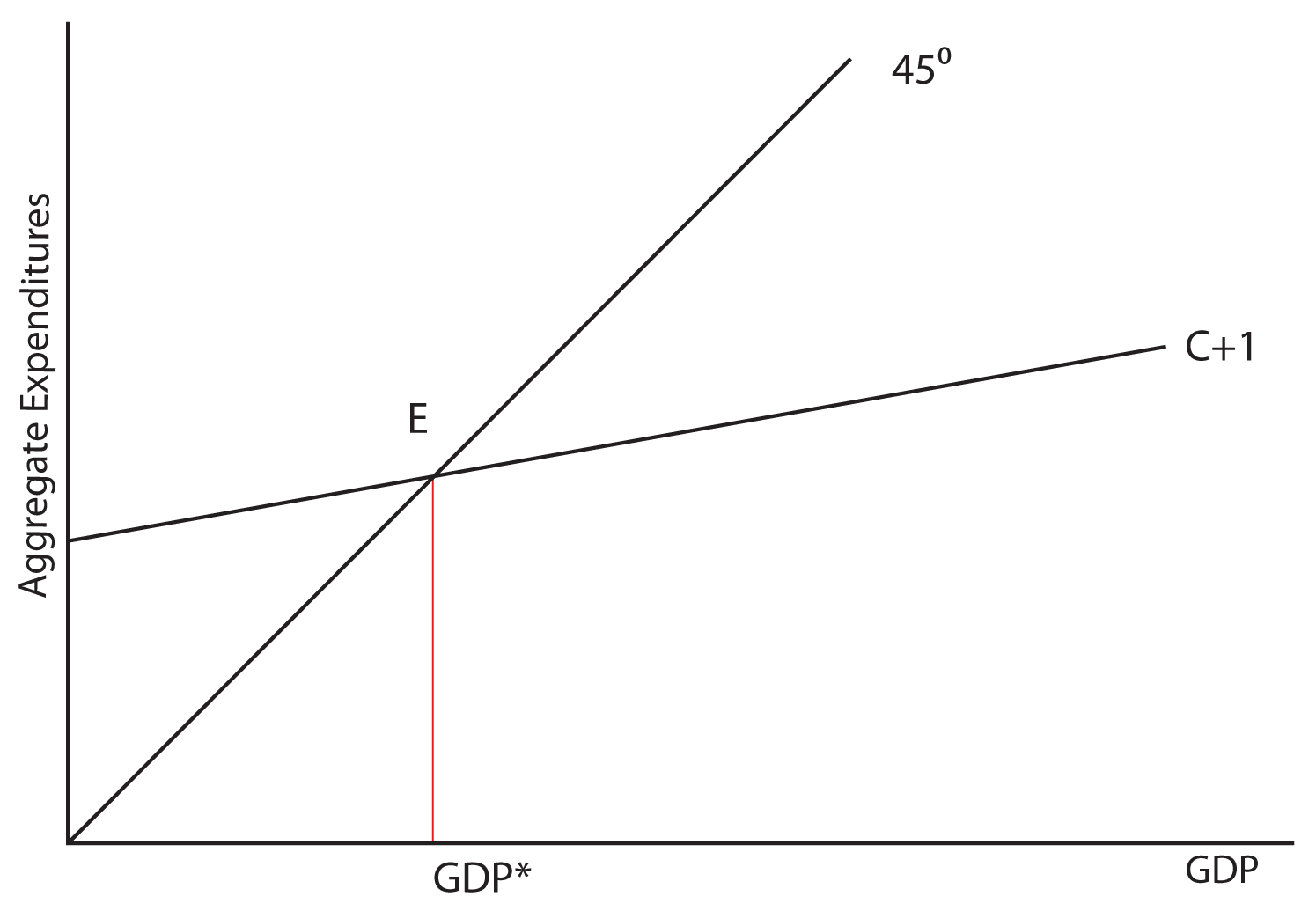
In the above graph, we labeled point E as the equilibrium point and GDP* as the equilibrium level of the GDP. Let’s explore why E is equilibrium. Remember that one of the characteristics of equilibrium is that if you move away from it, natural market forces should automatically move you back toward the equilibrium. Observe this process in the graph below:
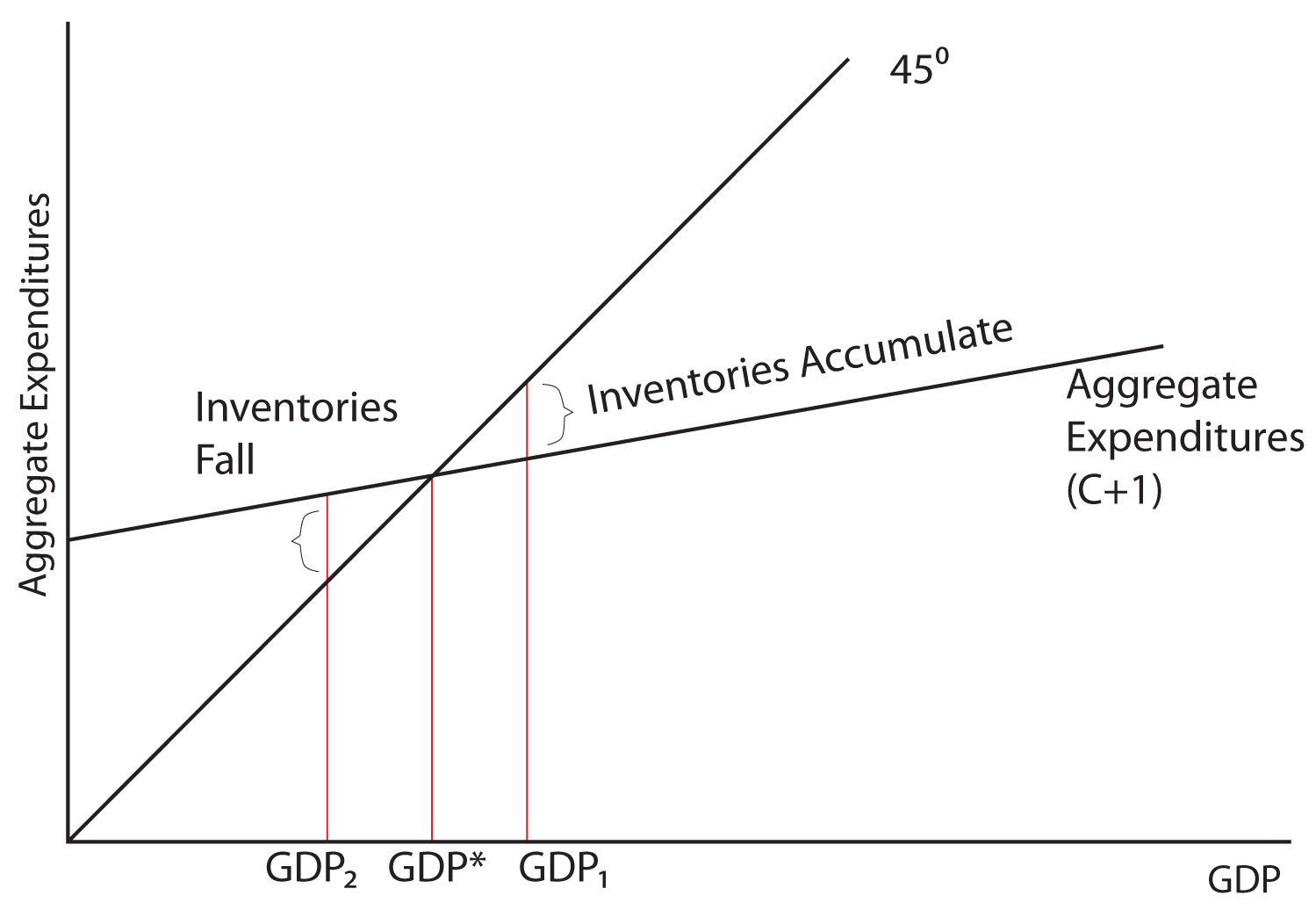
If the economy were for some reason producing at GDP1 instead of GDP*, what would be the result and what market forces might induce the economy to return to GDP*? Notice: at GDP1, total spending is less than output. We know that spending is less than output because at this level of GDP the Aggregate Expenditures line is below the 45 degree line, which is the line where spending is equal to output. So spending would be equal to output at point A, but actual spending as measured by the Aggregate Expenditures line is below that (labeled B). Imagine you are running the economy. Each month, you are producing 10,000 units of output and people are buying 9,000 units of output. Each month, you would be adding 1,000 units of output to your inventories and over the course of the year, inventories would be piling up. Imagine that producers have a certain level of inventories that they desire to have on hand, but that they do not want the stock of inventories to substantially grow or depleted. At GDP1, inventories would be piling up at the rate of 1,000 extra units of inventory each month! What would you do if you were running the economy and unwanted inventories were building up? Wouldn’t that be a signal to you to reduce production? As you reduce production, output or the GDP, falls from GDP1 to GDP*.
What if the economy were producing at GDP2? Now the Aggregate Expenditure line is above the 45 degree line, indicating that spending is above output. Spending would be equal to output at point D, but actual spending is at point F. Imagine that the economy is producing 5,000 units of output each month, but that consumers and businesses together are purchasing 6,000 units of output. How would it be possible for more to be bought than what is produced in any given time period? It would be possible if businesses have unsold inventories on hand. But if a business has an ideal level for their inventories that they want to maintain, and purchases exceed production, inventories will be drawn down or depleted. What would naturally happen in an economy if spending were greater than production and inventories were falling? Businesses would begin to produce more, and the output or GDP of the economy would rise from GDP2 to GDP*.To summarize, notice that in this model:
- If spending is greater than production, inventories will be depleted and production will rise, and
- If spending is less than production, inventories will accumulate and production will fall, SO ...
- Equilibrium is achieved where production exactly equals spending:
- Or, in other words,
Output = Spending
GDP = Consumption + Investment
GDP* is the equilibrium output of the economy because it is where output (GDP) is equal to spending (consumption + investment).
Savings and Investment
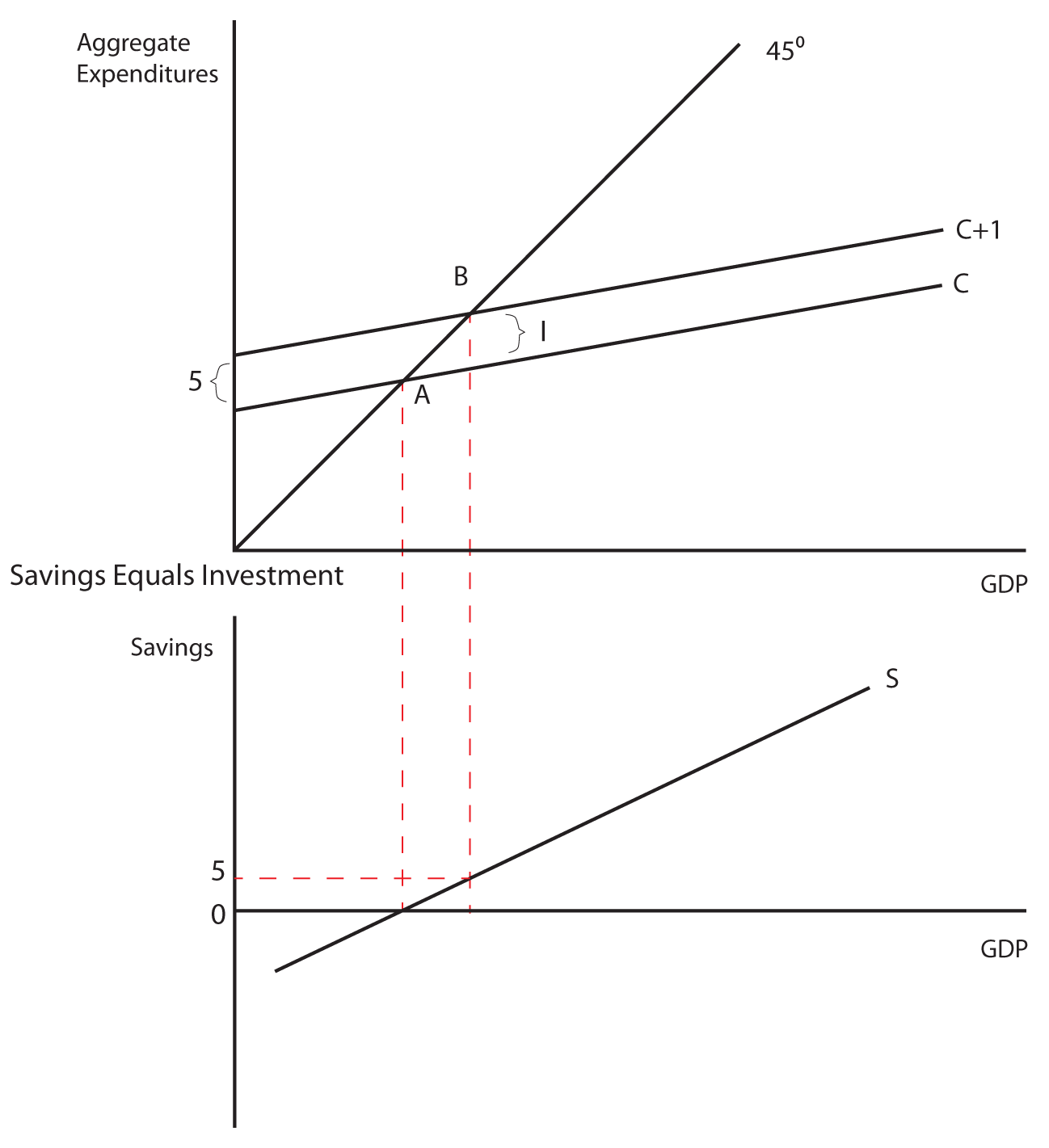
A second way of looking at equilibrium is through savings and investment. Remember that when people save, they are withdrawing spending from the flow of income and expenditures. Savings is therefore called a leakage. When businesses invest, they are adding spending to the flow of income and expenditures so that Investment is called an injection.
Equilibrium output is achieved when:
Leakages = Injections
or
Savings = Investment
If savings is greater than investment, then GDP is too high and output will fall. If savings is less than investment, then GDP is too low and output will rise. Let’s look at this graphically.
Think About It: Aggregate Expenditures
In the table below is data for a hypothetical private-closed economy. Private means that there is no government and closed means that there is no foreign trade. We will consider a mixed (both a private and a government sector) and open (one that accounts for foreign trade) economy later. Use the information in this table to graph the aggregate expenditures line on one graph and the savings and investment schedules on another graph. Show how these graphs illustrate that the aggregate expenditures of the company are in equilibrium. This means “spending equals output” is the same thing as “savings equals investment.”
| Real GDP | Consumption | Savings | Investment | AE = C + I |
|---|---|---|---|---|
| 11,800 | 12,000 | (200) | 600 | 12,600 |
| 12,600 | 12,600 | 0 | 600 | 13,200 |
| 13,400 | 13,200 | 200 | 600 | 13,800 |
| 14,200 | 13,800 | 400 | 600 | 14,400 |
| 15,000 | 14,400 | 600 | 600 | 15,000 |
| 15,800 | 15,000 | 800 | 600 | 15,600 |
| 16,600 | 15,600 | 1,000 | 600 | 16,200 |
The model of Aggregate Expenditures that we are currently considering is often called a Keynesian Model because it was first formulated by British economist John Maynard Keynes in his General Theory of Employment, Interest, and Money, published in 1936—at the height of the great depression. One of the central premises of Keynesian economics is the idea of a multiplier. Keynes hypothesized that a given increase in spending would cause output to increase by a multiple of the increase in spending. How is this possible?
Let’s start with the case of Investment spending. When a business spends $1 on new plant or equipment it injects $1 into the economy. That $1 becomes income to someone (whoever built the machine or constructed the new plant) who spends a portion of it and saves the rest. The portion they spend and the portion they save depends on their MPC and their MPS. The portion that is spent becomes income to someone else who likewise spends a portion, which becomes income to another, who spends a portion, and so on. The spending stream can be characterized in the following way:
$1 + $1(MPC) + $1(MPC)(MPC) + $1(MPC)(MPC)(MPC) + …
Or
$1 + $1(MPC) + $1(MPC)2 + $1(MPC)3 + …
Which can be shown in its limit to equal 1/(1-MPC). This is called the Investment Multiplier. As long as the MPC is less than 1, the multiplier will be greater than one. In fact, we can show that- When the MPC is .9, the multiplier is 10
- When the MPC is .8, the multiplier is 5
- When the MPC is .75, the multiplier is 4
- When the MPC is .6, the multiplier is 2.5
- When the MPC is .5, the multiplier is 2
It should also be stated that the investment multiplier can be shown in terms of the MPS. It is the reciprocal of the MPS, 1/MPS, since the MPS is equal to 1-MPC.
Example
Let’s consider a scenario where firms in the economy decide to increase investment spending by five million dollars. If the MPC is equal to .75, the Investment Multiplier is equal to four and output in the economy will go up by 20 million dollars (the five million dollar increase in Investment times the multiplier of four). Graphically this is shown below:
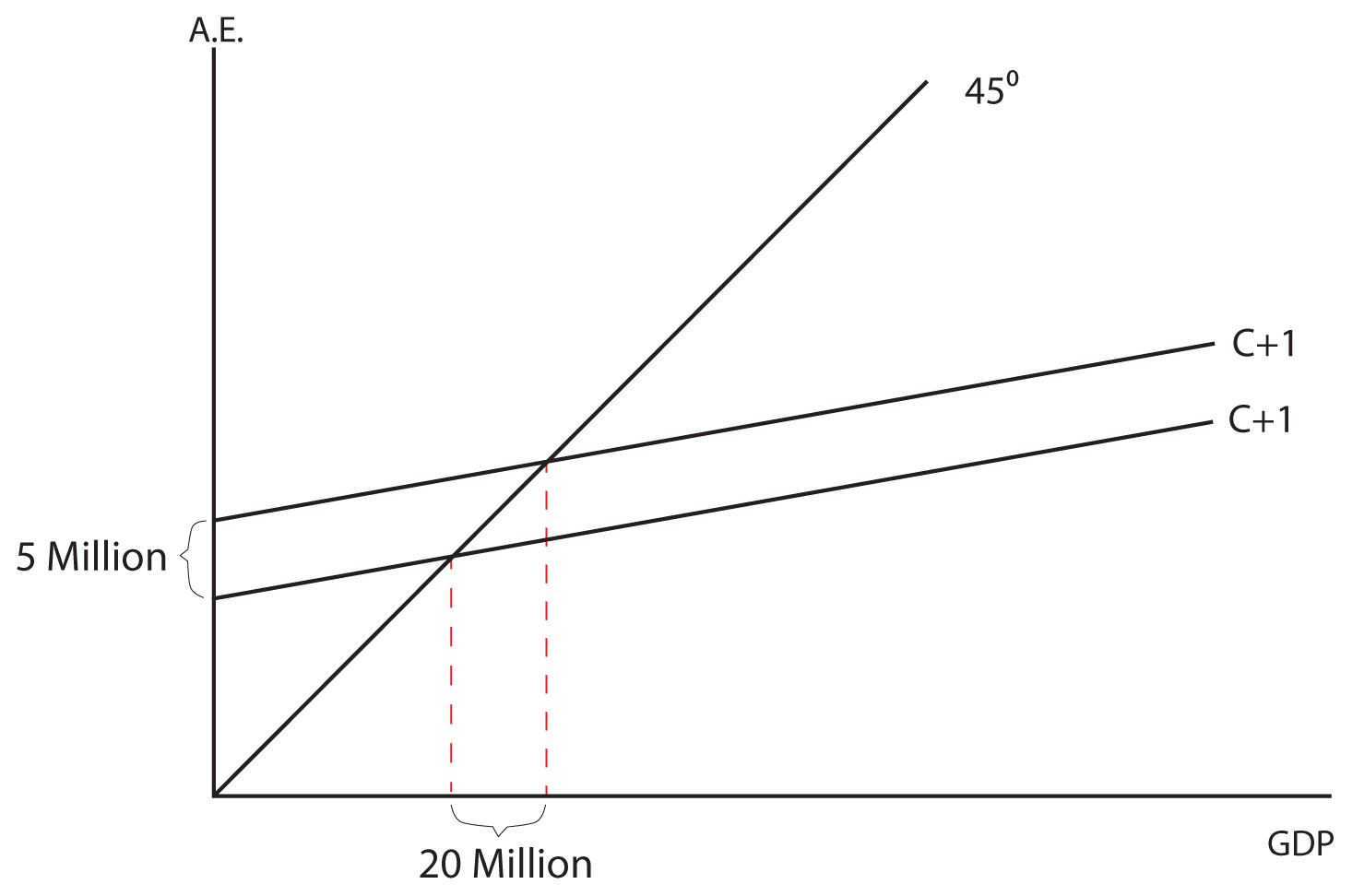
Think About It: Investment Multiplier Calculations
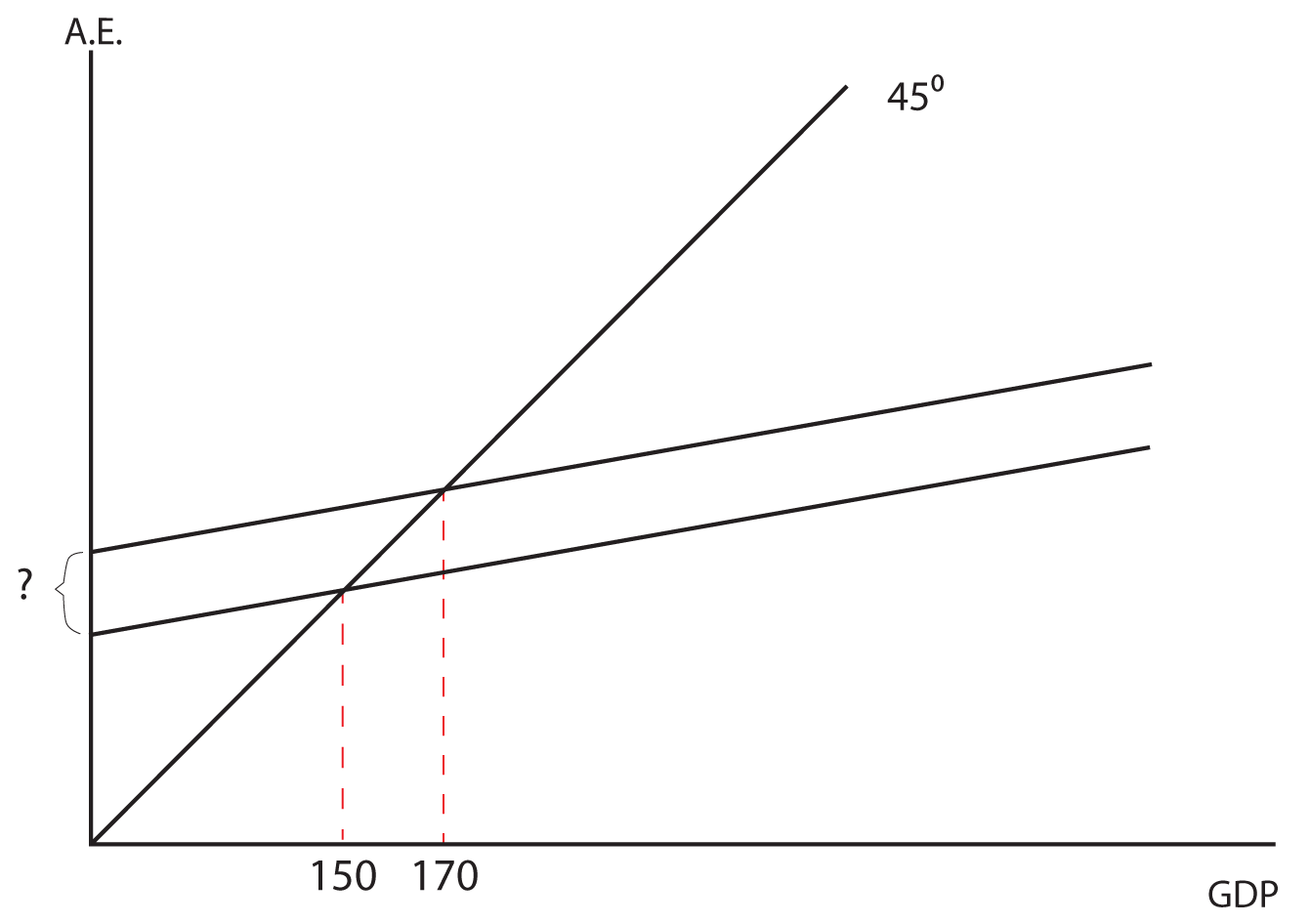
Based on the graphs given, answer the following questions.
1. In the first graph, if the MPC is 0.75, what is the new level of GDP when aggregate expenditures go up by two million?
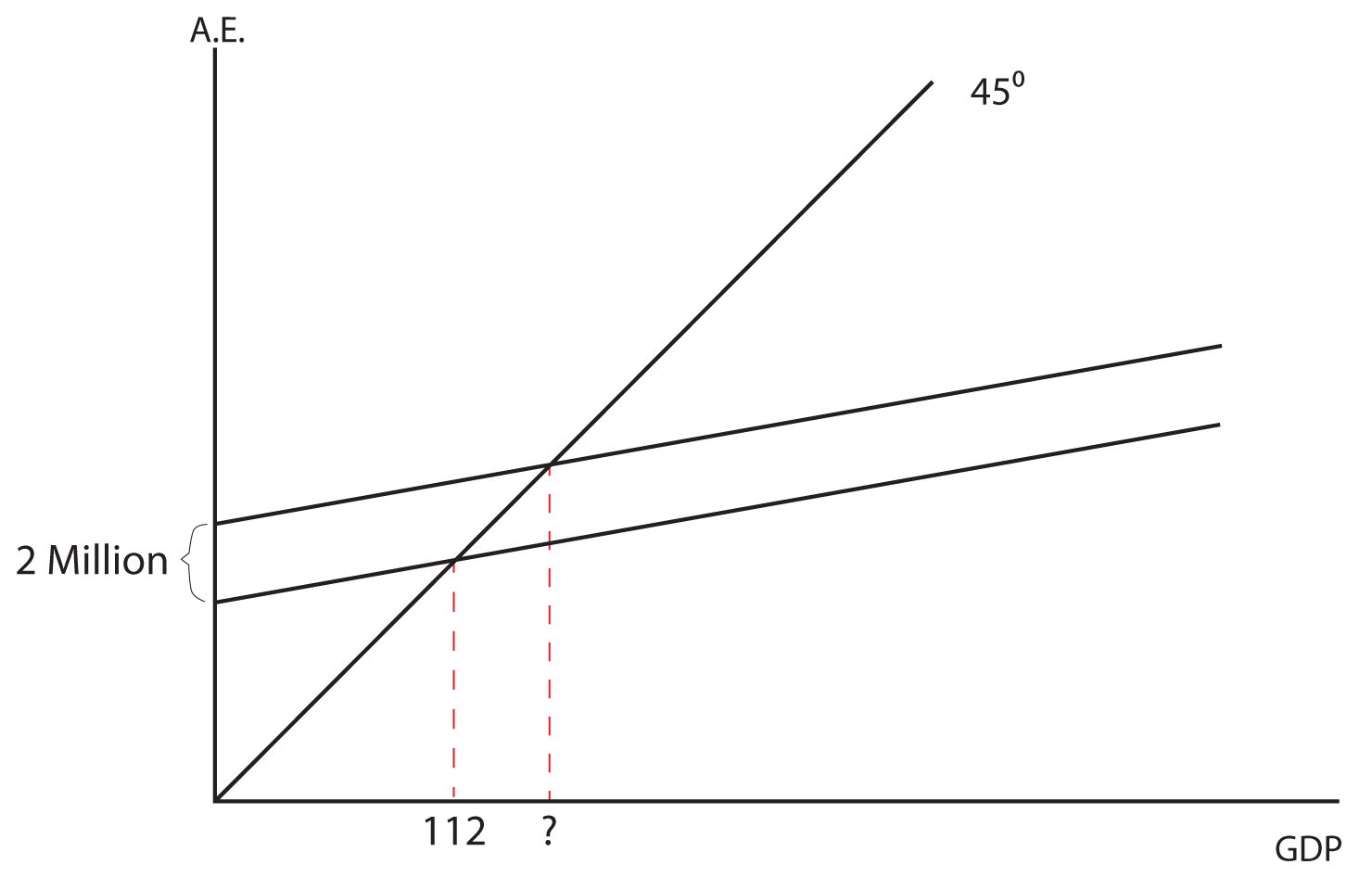
2. In this graph, what is the multiplier and what is the MPS?

3. In this graph, if the MPS is 0.2, how much did aggregate expenditure go up by to get the indicated increase in GDP?
Section 02: Government Spending
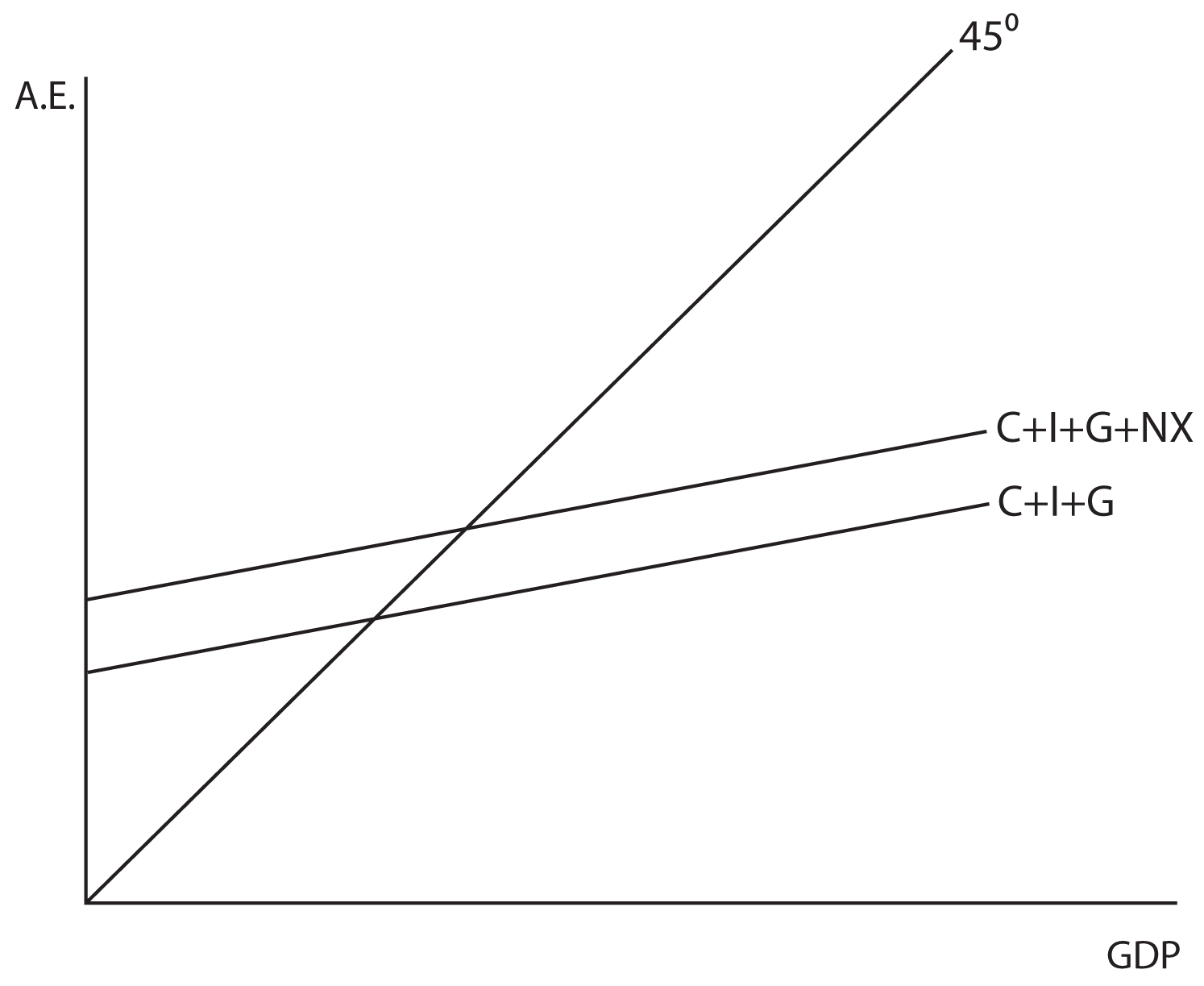
Now let us consider a mixed (both government and private spending) closed (no net exports) economy. The basic change is that we are now adding government spending to the model. Since government spending is determined by a political process and is not based on the level of the GDP, it is graphed as a horizontal line when GDP is on the horizontal axis. When this horizontal line is added to the upward sloping Aggregate Expenditures line, it simply shifts Aggregate Expenditure upward by the amount of the government spending. See the two graphs below for an illustration. The equilibrium GDP will be determined by where the C+I+G line intersects the 45 degree line in our standard model.

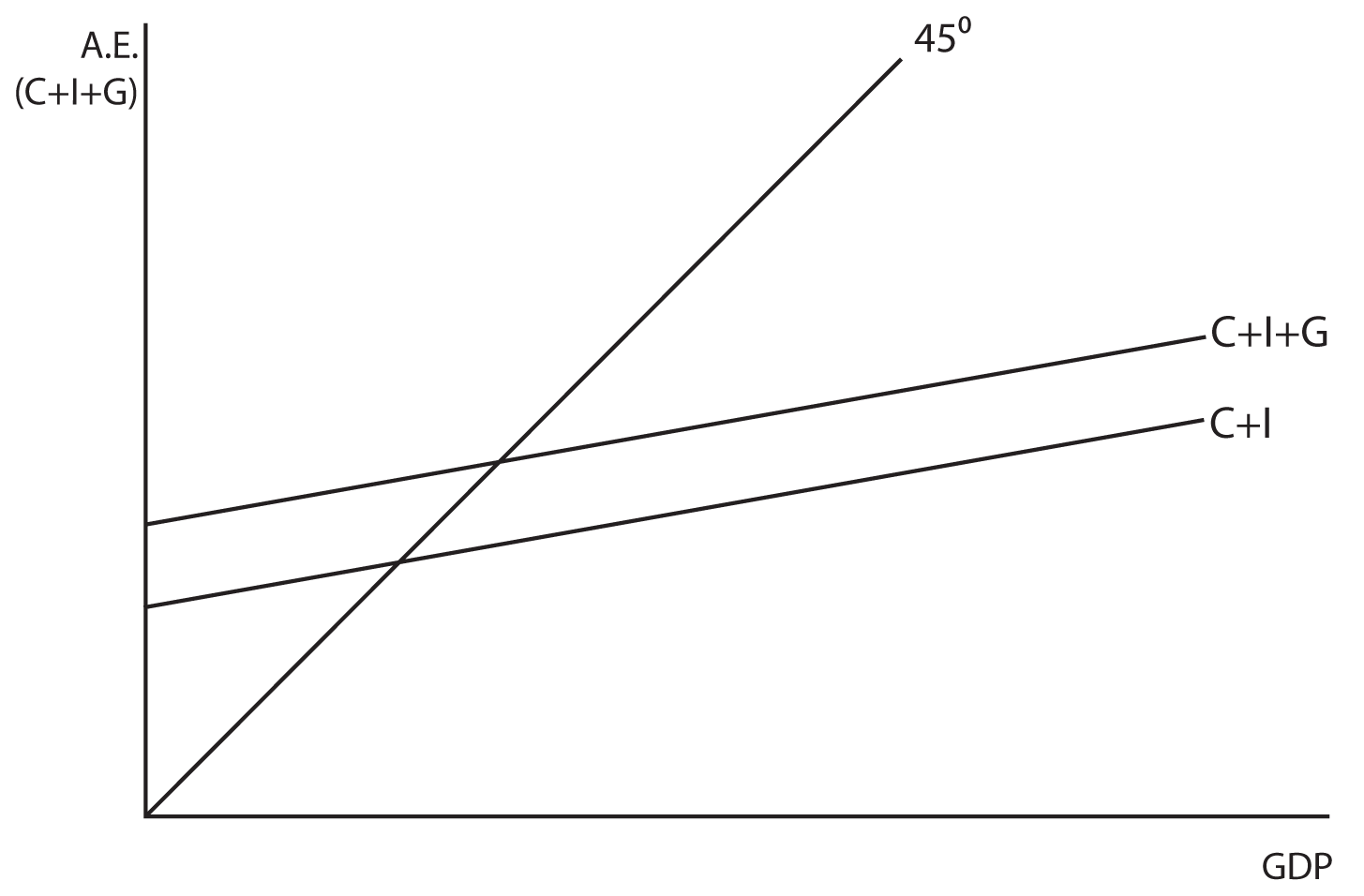
Changes in government spending have a similar impact on equilibrium GDP as changes in investment.
The Government Spending Multiplier
Quantitatively, the government spending multiplier is the same as the investment multiplier. A $1 increase in government spending will result in an increase in GDP equal to $1 times 1/(1-MPC). Since the investment and government spending multipliers are the same, they are sometimes just jointly referred to as expenditure multipliers.
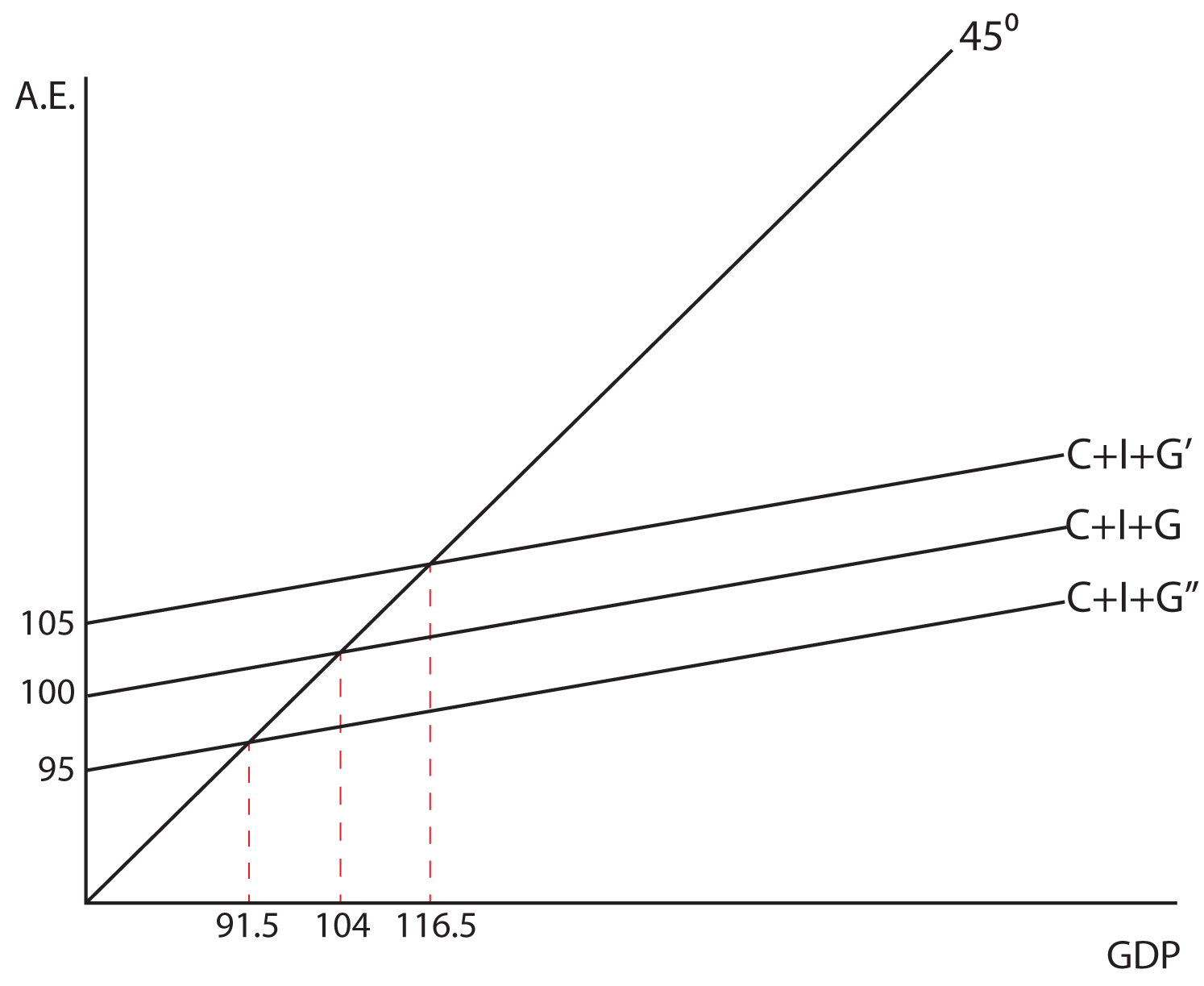
Think About It: The Effects of Government Spending
This example will illustrate the impact Keynes felt a change in government spending would have on output in the economy. Assume that the MPC is equal to 0.6. What does the government spending multiplier equal? What impact would a $5 billion increase in government spending have on equilibrium GDP? What about a $5 billion decrease in G? Can you illustrate both cases with a graph?
The Tax Multiplier
As mentioned before, the spending multipliers are all the same, 1/(1-MPC). There is also a multiplier that is associated with a change in taxes. It is called the tax multiplier, and it is NOT the same as the spending multipliers. In fact, it is smaller than the spending multipliers. Why would the tax multiplier be smaller than the government spending multiplier? The answer lies in the fact that when a business or the government undertakes new spending, they inject the initial amount of that spending into the income stream and then it multiples through the economy. When the government decides to lower taxes, they are not injecting new money into the economy; they are simply deciding not to take money out of the economy that was already in the income stream. Individuals will then spend some portion of the money that they get to keep. So, if the government increases spending by $1 billion, the entire $1 billion is injected into the income stream. If they reduce taxes by $1 billion, only the MPC x $1 billion is injected into the income stream. Therefore, the impact of the tax multiplier is:
$1(MPC) + $1(MPC)(MPC) + $1(MPC)(MPC)(MPC) + …
This progression can be shown to be equal to the spending multiplier times the MPC, or
MPC x 1/(1-MPC)
Which is simplified as
MPC/(1-MPC)
Since reducing taxes increases income and vice versa, the tax multiplier is negative, i.e.
-MPC/(1-MPC)
Let’s look at some common values of the MPC and determine the tax multiplier for each.
- When the MPC is .9, the tax multiplier is -9
- When the MPC is .8, the tax multiplier is -4
- When the MPC is .75, the tax multiplier is -3
- When the MPC is .6, the tax multiplier is -1.5
- When the MPC is .5, the tax multiplier is -1
Do you see the relationship between the expenditures multipliers and the tax multiplier at each level of the MPC? How would you describe it?
Note that a change in taxes shifts C in our aggregate expenditures model. An increase in taxes shifts C downward and a decrease in taxes shifts C upward with the expected impacts on equilibrium GDP.
Think About It: Production Possibilities
Show how a change in taxes has a specified impact on GDP, depending on the MPC. Show that you can get the same answer on its impact on GDP, using the tax multiplier or the expenditures multiplier. For example, let’s say the government increases taxes by $16 Billion with an MPC = 0.75. What impact would this have on equilibrium GDP?
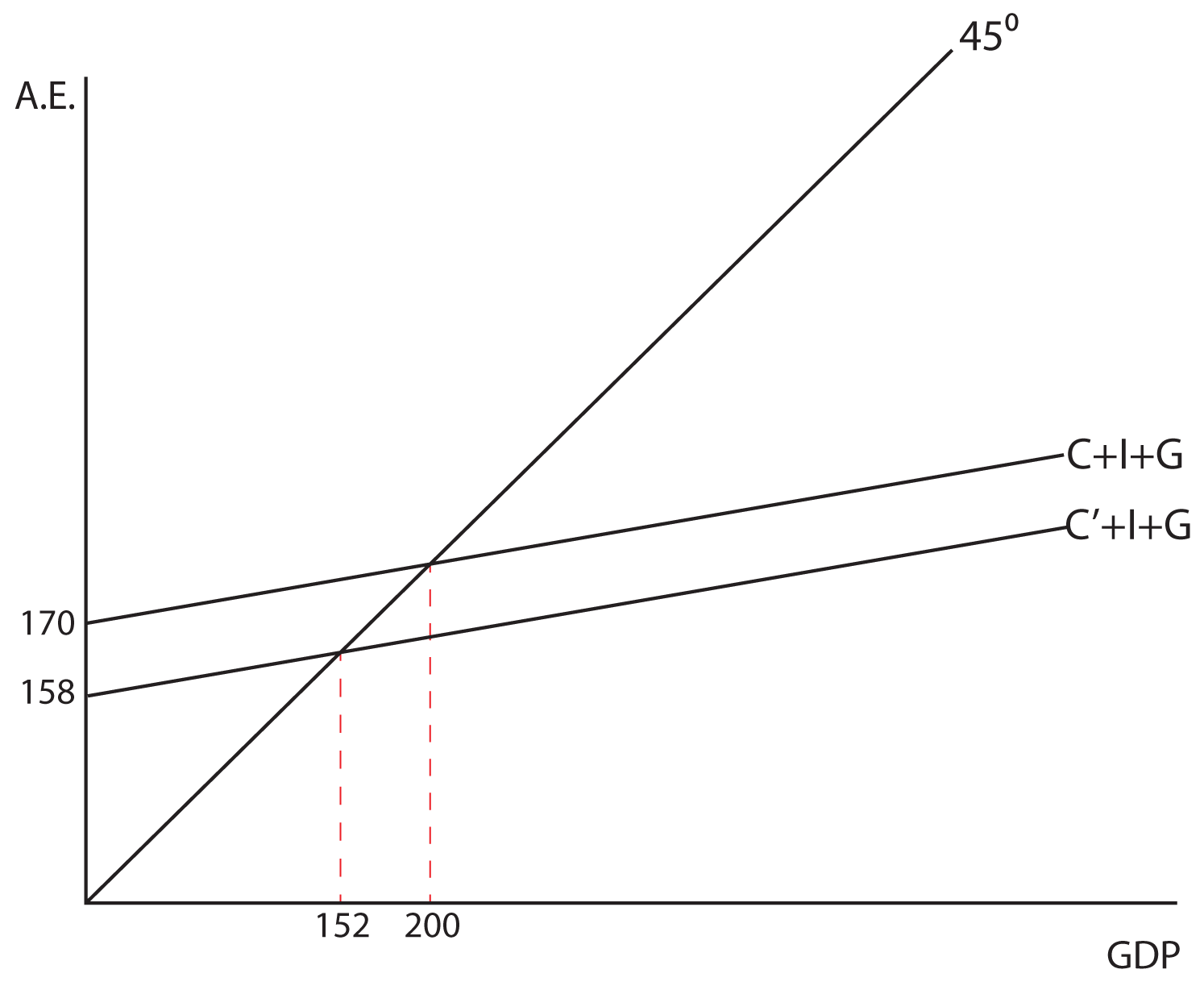
In the Lesson on Fiscal Policy, we will show how both government spending and taxes (the two primary components of fiscal policy) can be used to expand or contract the economy.
The Balanced-Budget Multiplier
The final multiplier we want to consider in the Keynesian Model is called the balanced-budget multiplier. Essentially, this multiplier tells us what the impact will be on the GDP if you increase both government spending and taxes equally. For example, if the government wanted to increase government spending by, let’s say, $2 billion, but did not want to run a deficit, and therefore also increased taxes by $2 billion. We’ll look at each of these actions independently and then put them together to find a generalized answer.
Assume the MPC is equal to .8. With an MPC of .8, the government spending multiplier is 5—if the government increases spending by $2 billion, output will go up by $10 billion. If the MPC is .8, the tax multiplier is -4—if the government increases taxes by $2 billion, output will go down by $8 billion. When these two things happen simultaneously, the net effect is to increase output by $2 billion ($10 billion - $8 billion = $2 billion). So an increase in government spending by $2 billion and a simultaneous increase in taxes by $2 billion will increase output by $2 billion. The balanced-budget multiplier is equal to 1 and can be summarized as follows: when the government increases spending and taxes by the same amount, output will go up by that same amount. We can generally show that the balanced budget multiplier is equal to one, and that it is not dependent on the size of the MPC: when you sum the spending multiplier and the tax multiplier, you always get one, regardless of the MPC.
1/(1-MPC) – MPC/(1-MPC) = (1-MPC)/(1-MPC) = 1
Think About It: Calculating the Effect of the Balanced Budget Multiplier
Demonstrate both graphically and algebraically the impact on GDP of increasing government spending and taxes by $5 billion dollars when the MPC is .9.
Section 03: The Recessionary and Inflationary Gaps
Let’s say that GDP = 1400 is the full employment output, or the equilibrium level we would like to obtain. Also assume that the MPC is equal to .6. If the economy was actually producing 1300 and the government wanted to implement policies to increase output to 1400 they would need to increase government spending by 40. This additional 40 in government spending is called the recessionary gap.

To change output in the economy from 1500 to 1400 you would have to reduce G by 40. In this case, the 40 in government spending is an inflationary gap.
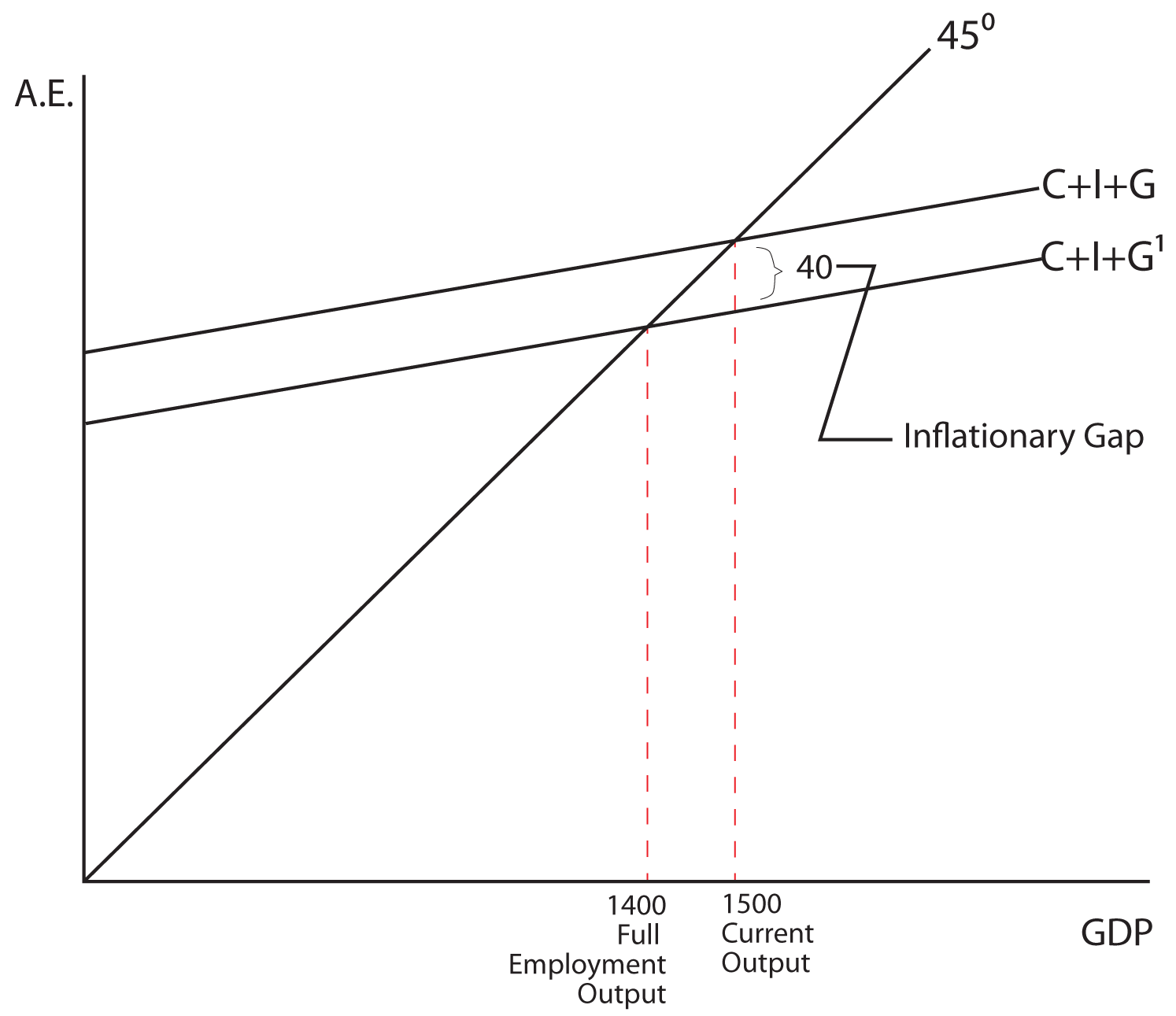
When G is used to increase output, it is called anti-unemployment policy and when G is used to decrease output it is called anti-inflationary policy.
Net exports and Equilibrium Output
If we add international trade to our analysis and assume that net exports are independent of the level of GDP, then equilibrium GDP will be determined by where the C+I+G+NX line intersects the 45 degree line in our standard model (see the graphs below).
Changes in NX have a similar impact on equilibrium GDP as changes in investment or government spending have. For example, if the MPC were equal to 0.5 and there were an increase in NX equal to $15 million, the output would increase by $30 million. This is true because the multiplier would be equal to 2.