Production Functions
We are now going to focus on the what is behind the supply curve. Profits equal total revenue minus total costs. Total revenue is equal to price times quantity and we examined their relationship in the elasticity section. This section focuses on the second part of the equation, costs. In order to produce, we must employ resources, i.e., land, labor, capital, and entrepreneurship. What happens to output as more resources are employed?
We can demonstrate the impact of adding more of a variable resource, say labor, to a fixed amount of capital and see what happens to output. For demonstration purposes in economics, we often make widgets, which is really any hypothetical manufactured device. Our widget will be made taking a quarter sheet of paper, folding it in half twice then stapling it and writing the letter W on it. If you have a big family, you can do this as a Family Home Evening activity; otherwise you can just read along to see the results. The inputs are a stack of quarter sheets of paper, one stapler, one pen, and a 2’ x 3’ sheet of poster board which represents your factory wherein all production must take place. Each round is a certain amount of time, say 40 seconds.
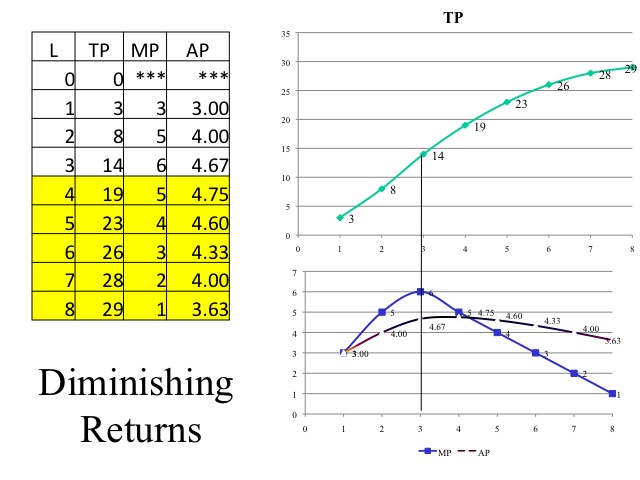
What will be the output level of widgets as more labor is added? With zero workers, nothing gets produced. With one worker, the worker must fold the paper, staple it, and write the W. Doing all of these tasks by himself, our first worker is able to produce three widgets.

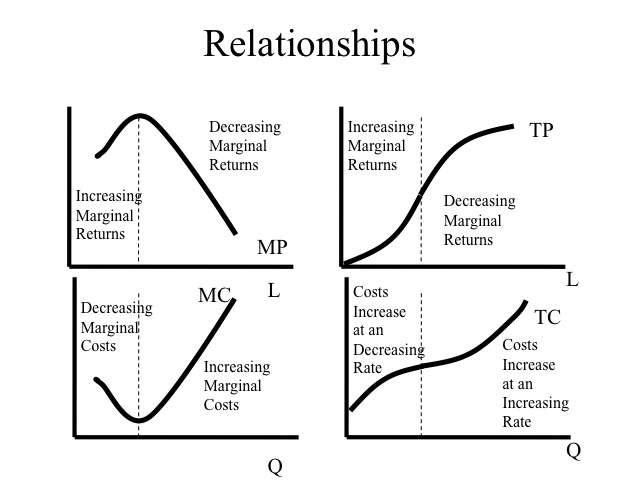
Total product is simply the output that is produced by all of the employed workers. Marginal product is the additional output that is generated by an additional worker. With a second worker, production increases by 5 and with the third worker it increases by 6. When these workers are added, the marginal product increases. What factors would cause this? As more workers are added, they are able to divide the respective tasks and specialize. When the marginal product is increasing, the total product increases at an increasing rate. If a business is going to produce, they would not want to produce when marginal product is increasing, since by adding an additional worker the cost per unit of output would be declining.
In The Wealth of Nations, Adam Smith wrote about the advantages of the division of labor using the example of a pin maker. He pointed out that an individual not educated to the business could scarce make one pin a day and certainly not more than twenty. But the business of pin making is divided up into a number of peculiar trades and each worker specializes in that trade. “One man draws out the wire, another straights it, a third cuts it, a fourth points it, a fifth grinds it at the top for receiving the head; to make the head requires two or three distinct operations; to put it on, is a peculiar business, to whiten the pins is another; it is even a trade by itself to put them into the paper; and the important business of making a pin is, in this manner, divided into about eighteen distinct operations, which, in some manufactories, are all performed by distinct hands, though in others the same man will sometimes perform two or three of them.” As a result, these ten people are able to produce upwards of forty-eight thousand pins in a day.
Reference: http://www.econlib.org/library/Smith/smWN1.html#B.I,%20Ch.1,%20Of%20the%20Division%20of%20Labor

At some point, diminishing marginal returns sets in and the marginal product of another worker declines. As more workers are added, the capital, i.e., factory size, stapler and pen become more scarce. The law of diminishing marginal returns states that as successive amounts of the variable input, i.e., labor, are added to a fixed amount of other resources, i.e., capital, in the production process the marginal contribution of the additional variable resource will eventually decline. As the marginal product begins to fall but remains positive, total product continues to increase but at a decreasing rate. As long as the marginal product of a worker is greater than the average product, computed by taking the total product divided by the number of workers, the average product will rise. For students, it is often easiest to remember when you think about your grade point average. If your g.p.a. for this semester, i.e., your marginal g.p.a., is greater than your cumulative g.p.a., i.e., your average g.p.a., then your average g.p.a. will rise. But if your g.p.a. this semester is lower than your cumulative g.p.a., then your cumulative g.p.a. will fall. Thus the marginal product will always intersect the average product at the maximum average product.
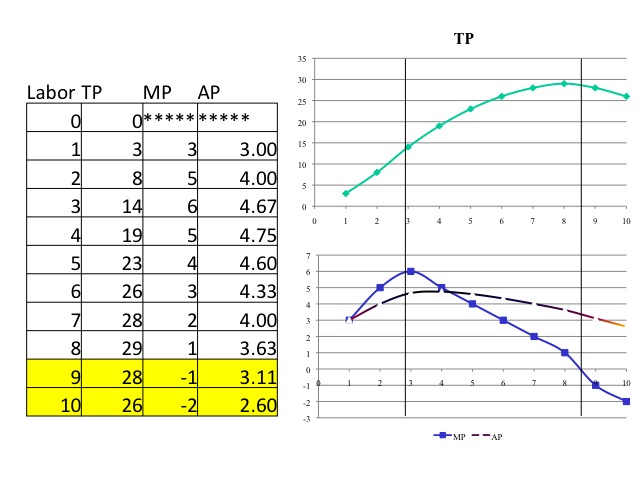
There may even come a point where adding an additional worker makes things so crowded that total product begins to fall. In this case the marginal product is negative. In our example, adding the ninth and tenth worker yields lower output than what was produced with only eight workers.
So how many workers should be employed? We know that we would not stop in the region where marginal product is increasing and we would not produce in the region where marginal product is negative. Thus we will produce where marginal product is decreasing but positive, but without looking at the costs and the price that the output sells for, we are unable to determine how many workers to employ.
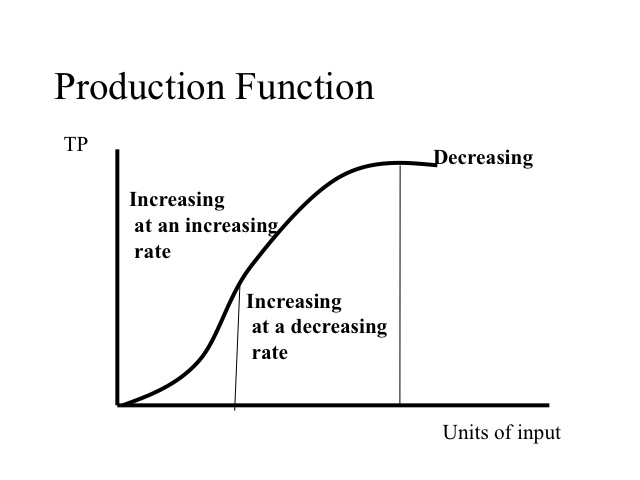
A production function shows the output or total product as more of the variable input, in our case labor is added. The function shows the regions of increasing marginal product, decreasing marginal product, and negative marginal product.
Practice
Residential construction crews are often three to eight people depending on the type of work. Think of what factors would cause increasing and decreasing marginal productivity in construction. Think of another industry and what would be the ideal number of workers?

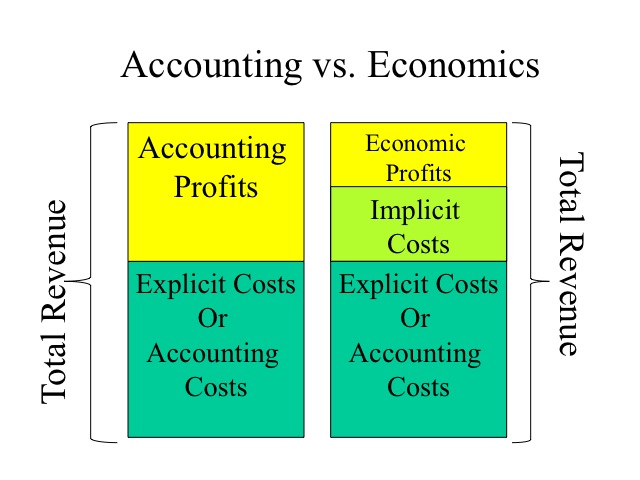
Accounting vs. Economics
Recall that explicit costs are out-of-pocket expenses, such as payments for rent and utilities, and implicit costs reflect the opportunity costs of not employing the resource in the next best option. Thus, the owner of building doesn’t have to pay rent, but by using the building foregoes the opportunity of renting the building out to someone else.
Accounting profits are calculating by subtracting the explicit costs from total revenue. Economic profits go a step farther and also subtract the implicit costs. By including implicit costs, we can then determine if the resources are earning at least what could be earned if employed in the next best option. A normal profit is the minimum return to maintain a resource in its current use. If a firm is earning zero economic profit would they still stay in business? A firm that is earning a zero economic is earning a normal profit and there is no incentive to move the resources to another use, since the amount that they are earning is equal to the return that could be earned elsewhere.
Practice
Using the information below, compute the explicit and implicit costs, the accounting and economic profits. Then explain what will happen in this industry and why.
Total Revenue $600,000
Cost of materials $200,000
Wages to employees $250,000
Foregone wage $100,000
Foregone rent and interest $80,000
The explicit costs would be the out-of-pocket expenses of materials and employee wages: 200,000 + 250,000 = $450,000. The implicit costs are the foregone opportunities, in this case the wage the owner is giving up by working in her business instead of working elsewhere and the foregone rent and interest that could be earned by the building and money tied up in the company - $100,000 + $80,000 = $180,000. The accounting profit is $150,000 computed by taking the total revenue $600,000 less the explicit costs $450,000. Subtracting the additional $180,000 of implicit costs leaves an economic profit of negative $30,000. Although the business owner is earning an accounting profit of $150,000, her economic profit is negative meaning that she could earn more by shutting down the business and employing the resources in their next best alternative. Thus if this loss continues, we would anticipate the owner would exit this business.
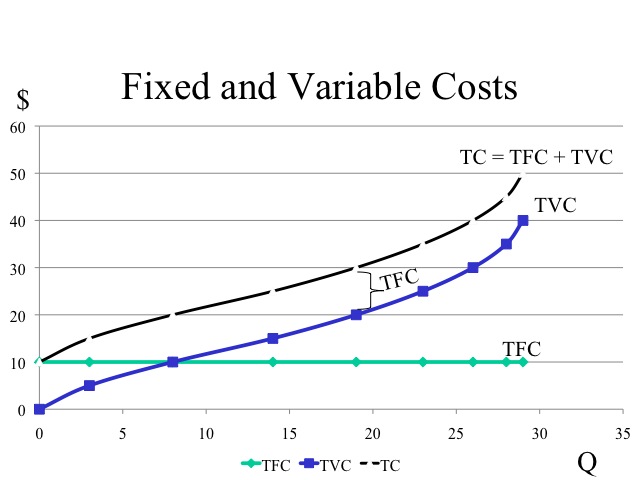
In the short run, at least one of the inputs or resources is fixed. Fixed costs are those that do not change as the level of output changes. Variable costs are those costs that change as output changes. Fixed costs can be quite large. In the airline industry, for example, fixed costs range from 40 to 70 percent of total costs. Thus during the week of September 11, 2001 when commercial flights were grounded, the airlines still incurred substantial costs even though they were not operating. These fixed costs included items such as insurance, depreciation on equipment, taxes, and interest on their loans. Since they were not operating, however, variable costs such as jet fuel, meals on board, and wages to hourly employees were not incurred.
Since fixed costs do not change as output changes, the total fixed cost line is flat at the level of fixed cost. If no production takes place, variable costs are zero. As production increases, total variable costs increase at a decreasing rate, since the marginal product for each additional worker is increasing. With diminishing marginal product, the total variable cost increases at an increasing rate. Total costs is the sum of total fixed costs and total variable costs, thus total cost begins at the level of fixed costs and is shifted up above the total variable cost by the amount of the fixed cost.
Reference: http://www.accenture.com/Global/Research_and_Insights/By_Industry/Airline/AirlinesOutsourcing.htm
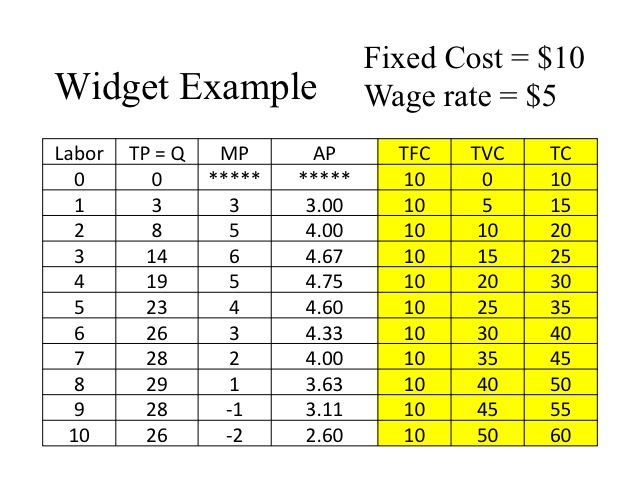
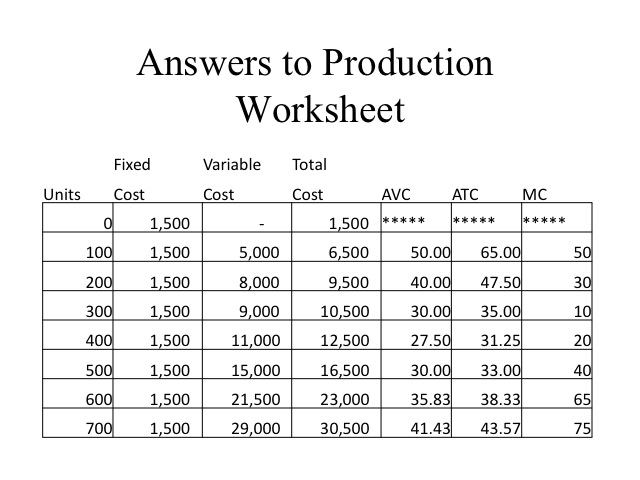
In our widget example, we will assume that the fixed cost for the stapler, pen, and “factory” is $10 and the cost of each worker hired is $5 per worker. Since fixed costs are constant, the firm incurs $10 regardless of the level of output. Labor is the only variable cost computed by $5 times the number of workers. When we discuss costs, we are going to refer to our output as quantity denoted by a Q, instead of total product, denoted by the TP.
We can also evaluate costs looking at the marginal costs and average costs. Marginal cost is the change in total cost divided by the change in output. Since fixed costs do not change with output, marginal cost can also be computed by dividing the change in total variable cost by the change in quantity. If the equation, TC = TFC and TVC is divided by quantity, we get the average of each item, i.e., average total cost equals average fixed costs plus average variable cost.

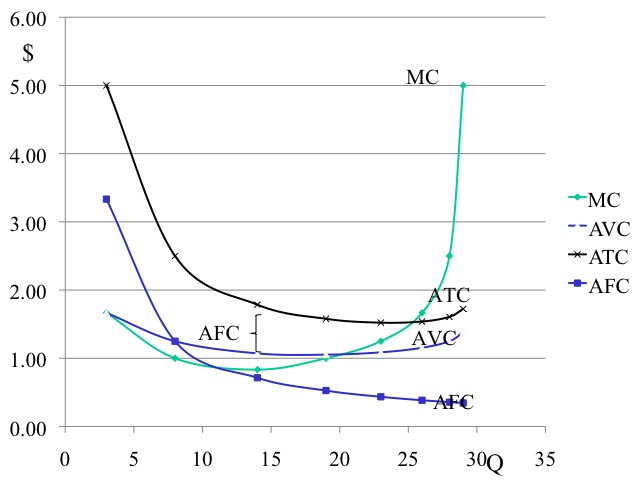
Using our widget example, we compute the MC, AFC, AVC, and ATC. Note that we did not compute the marginal or average values at zero output.
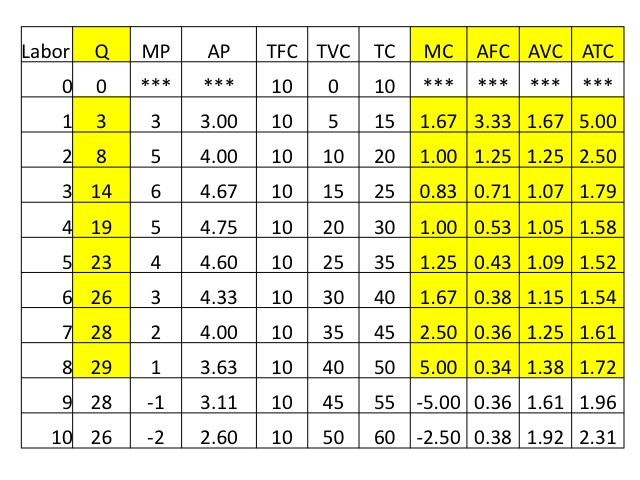
It is often easier to see important relationships when we graph the results for ATC, AVC, AFC, and MC. Keep in mind that we never produce where marginal product is negative, i.e., in our example we would never employ the ninth and tenth worker. So we will graph only the output of one to eight workers. We often do not graph the average fixed costs, because average fixed cost is represented by the vertical distance between ATC and AVC. However, in this case we will graph it so that you can see an important feature: since fixed costs don’t change with the level of output, average fixed costs get smaller as more quantity is produced, making the vertical distance between ATC and AVC smaller as output increases. Another important relationship can also be seen in these figures, and that is marginal cost intersects average variable and average total costs at their minimums. Recall that a similar observation was made for marginal product and average product, only in that case, marginal product intersected average product at its maximum.
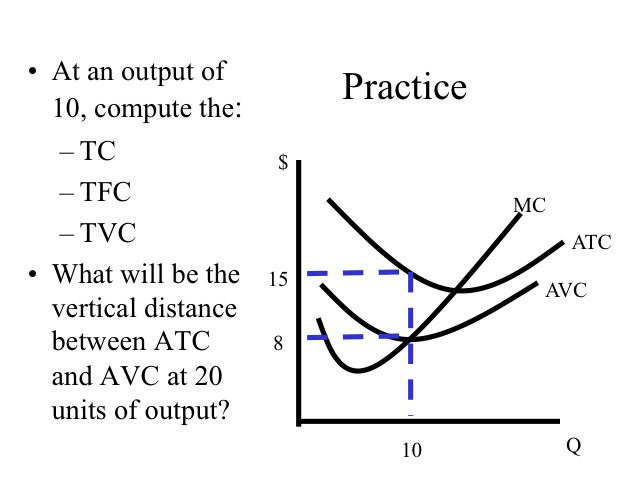
Practice
1. At an output of 10, compute the (a) TC, (b) TFC, and (c) TVC.
2. What would be the vertical distance between ATC and AVC at 20 units of output?
Answers
Total Cost = ATC*Q = $15*10 = $150
Total Variable Cost = AVC*Q = $8*10 = $80
The vertical distance between ATC and AVC is AFC, so TFC = AFC*Q = $7*10 = $70
If the total fixed cost is $70 then at 20 units of output, the vertical distance between ATC and AVC which is the AFC would be $3.50.
Some important relationships exit between the productivity measures (TP, AP, and MP) and the cost measures. These relationships result from how productivity determines costs. Consider, for example, when a business adds one more worker who causes productivity to improve. This would mean that output is increased more for this worker than for previous workers! On the margin, what do you think will happen to the additional cost with respect to output? Clearly the cost of that additional output will be lower because the firm is getting more output per worker. This results provides an interesting relationship between marginal cost and marginal product. When marginal product is at a peak, then marginal cost must be at a minimum. This will always hold true, and as a result, marginal cost is the mirror image of marginal product. When marginal product is rising, the marginal cost of producing another unit of output is declining and when marginal product is falling marginal cost is rising. Similarly, when average product is rising, average variable cost is falling, and when average product is falling, average variable cost is rising (since average product corresponds the variable input changing, this important relationship exists with average variable cost and NOT average total cost). Finally, when total product is increasing at an increasing rate the total cost is increasing at a decreasing rate. When total product is increasing at a decreasing rate, the total cost is increasing at an increasing rate.
Practice
1. Complete the following worksheet. Use the equations below to help you complete the worksheet.
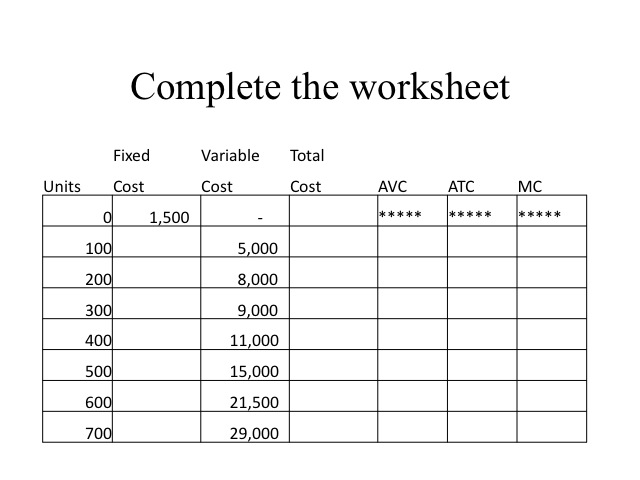

Answers to Production Worksheet
Cost Curves
The long run is that period of time that would allow all inputs or resources to become variable. In the long run, there are no fixed costs and a firm can decide the amount of each input. Think of a business just starting and they could determine the building size, the amount of equipment, the number of workers, etc. What would be the ideal quantity of each input?
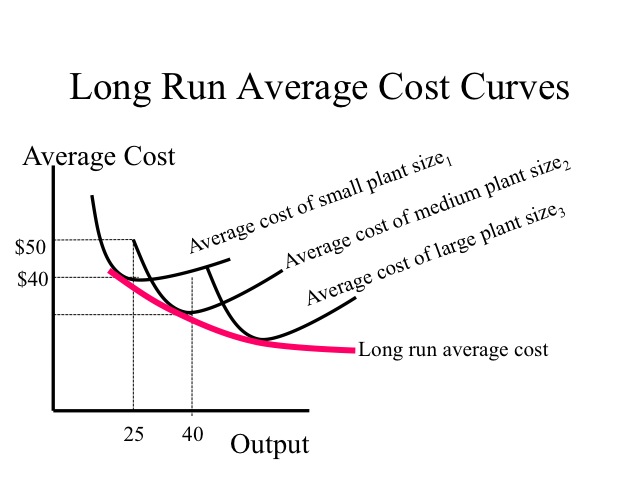
Up until now, we have been considering costs in the short-run, i.e. when at least one factor is fixed. Now we want to consider what happens to costs when all inputs are variable, i.e. the long-run. Typically, the plant size can only be changed in the long-run, that is, it is often the last input to become variable. In the long-run, we want to select a plant size that gives us the lowest costs for our level of output. For example, let’s assume we can build different sizes of a plant. If the desired output is only 25 units, then a small plant is able to produce at a lower average cost ($40) than the medium size plant ($50). However, if our desired output is 40 units, then the medium size plant is able to produce at a lower average cost than the small plant. Businesses often face the challenge of knowing what quantity of inputs (i.e., building and equipment size) to purchase that will allow them to be competitive today given their current market share, but still be able to grow and be competitive in the future as market share expands.

Assuming all factors are variable, the long run average cost curve shows the minimum average cost of producing any given level of output. The long-run average cost curve is obtained by combining the possible short-run curves (i.e. it is obtained by combining all possible plant sizes). More particularly, it is a line that is tangent to each of the short run average cost curves. If increasing output reduces the per unit cost, the firm is experiencing economies of scale (which means larger plant sizes have lower average total costs at their respective minimum points) . We typically see this when plant sizes are small.
This can be explained based on a variety of reasons. As plant capacity increases, firms are able to specialize their labor and capital to a greater degree. Workers can specialize on doing a limited number of tasks extremely well. Another factor contributing to economies of scale is the spreading out of the design and start up costs over a greater output amount. For many products, significant costs are in design and development. For example in the movie industry, the marginal cost of making a second copy of a movie is nearly zero and as copies of the movie are produced, the average cost declines significantly. Some film makers will film the movie and its sequel at the same time to lower the per unit costs.
As larger quantities are produced, the inputs used can be purchased in larger quantities and often at a lower per unit cost. The per unit cost when ordering a rail car or semi load of material is less than when purchasing the inputs in small quantities. Also spreading the cost of placing the order over more units, reduces the per unit cost.
Reference:
http://www.nytimes.com/2001/12/12/movies/gambling-film-fantasy-lord-rings-shows-new-line-cinema-s-value-aol.html?pagewanted=1
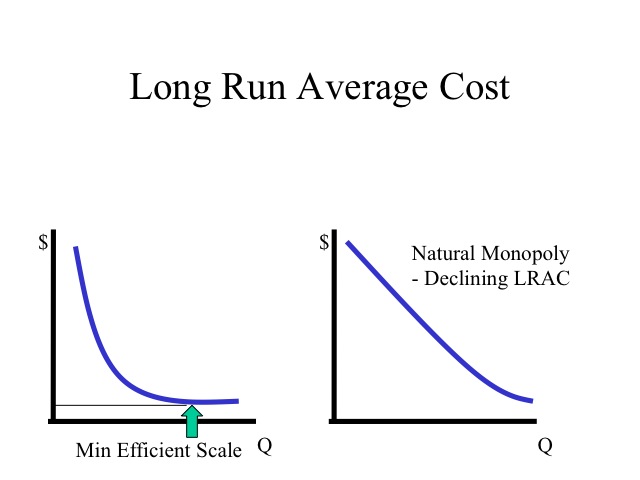
The cost structure of the industry determines the shape of its long run average cost curve. Some industries are able to reach the lowest per unit cost with a relatively small plant size or scale of operation. Other industries exhibit a natural monopoly where the long run average cost curve continues to decline over the entire range of a product demand. In this type of an industry, it is difficult for other firms to enter and compete since the existing firm has a lower per unit cost. The minimum efficient scale is the plant size (or scale of operation) that a firm must reach to obtain the lowest average cost or exhaust all economies of scales.
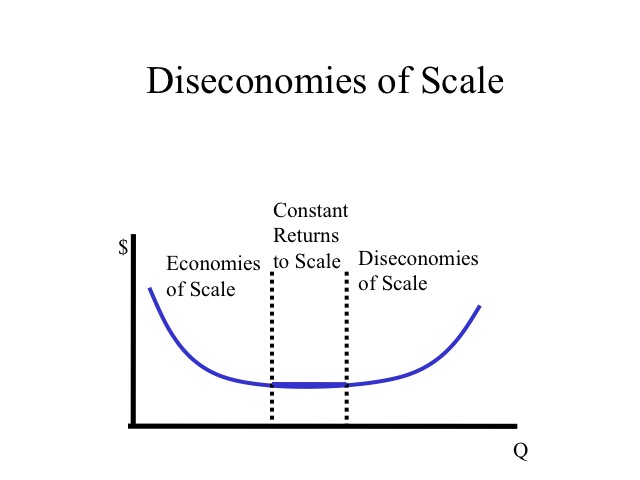
The region where long run average costs remain unchanged as plant size increases is known as constant returns to scale. Diseconomies of scale occurs when average costs increase as plant size increases. As output increases the amount of red tape would increase as it becomes necessary to hire managers to manage managers. Efficiency is lost as the size of the operation becomes too large. If an auto manufacturer decided to produce all of its output at one location, think of the size of the operation. Moving inputs into and out of the plant would raise costs significantly. Likewise, it would be difficult to find the needed workforce all in one city. Recognizing the diseconomies that could exist, auto manufacturers have instead chosen to produce their output at a number of different plants spread out throughout the world.
Consider another example. Think of what it would cost to make your own car. How many hours of design would it take? As you go to build the vehicle, think of the specialized tools that you would need to make the engine, frame, windows, ties, etc. Even if you built a car for each member of your family or every household in your town, the cost per vehicle would enormous because at this scale of operation, the degree of specialization is limited. Companies that do make cars produce thousands or even millions which allow them to specialize their capital and labor making the per unit cost significantly lower.
Think about this additional example. Why can film makers such as Disney or Pixar sell their movies that cost millions of dollars to make for $20 each, while technical education videos that cost a few hundred thousand to produce will sell for hundreds of dollars?
Popular movies will sell hundreds of thousands of copies, which allows the film makers to specialize their workforce and equipment since their scale of operation will be significantly greater. On the other hand, technical education films cost significantly less to produce but only a few hundred copies will be sold. Since their scale of operation is small, they are unable to gain the benefits of economies of scale that would allow them more efficient use of labor and capital.

While economies of scale lowers the per unit cost as more of the same output is produced, economies of scope lowers the per unit cost as the range of products produced increases. For example, if a restaurant that provides lunch and dinner began to offer breakfast, the fixed costs of the kitchen equipment and the seating area could be spread out over a larger number of meals served decreasing the overall cost per meal. Likewise a gas station that already must have a service attendant and building can lower the per unit cost by providing convenience store items such as drinks and snacks. Since the cost of producing or providing these products are interdependent, providing both lowers the cost per unit.