Chapter 3: Algebra
Section 3.1
3+ “what” = 7? If you have come through arithmetic, the answer is fairly obvious: 4.
However, if I were to ask something like:
2 times “what” plus 5 all divided by 7, then minus 6 = 5? There tends to be a little more difficulty in popping out the answer. The beauty of math is that it allows us to write down all of that stuff and then systematically make it simpler and simpler until we have only the number left. Wonderful.
We start with the easy ones to find out all of the rules and then we will build up to the big ones. 3+ “what” = 7
First, we need to adjust the fact that we are going to be writing “what” all the time. A very common thing is to put a letter in that place that could represent any number. We call that a variable. We replace the word “what” with “x” (or you could use p, q, r, f, m, l . . . ) So our equation becomes:
3 + x = 7
The whole goal of math is to find the number that makes that statement true. We already know that the number is 4. We would write:
x = 4
Now, look at what happened to our original equation. Do you see that the right side is missing a 3 and the left side is now 3 lower as well? This gives us some insight into what we can do to equations! Try another one:
x + 8 = 10
What number would make that statement true? If x were equal to 2, it would work. We write:
x = 2
Notice how we get the number that would work by subtracting that 8 from both sides of the equation.
Let’s see if it works with some other equations:
x – 7 = 2 and x – 3 = 10
With these two equations, the answers are:
x = 9 and x = 13
We got the answers by adding the 7 and the 3 to the right hand sides. This brings up a good point. In the first couple of equations that we did, we subtracted when the equation was adding. In the last two equations, we added when the equation was using subtraction. Let’s look at what happens when we start doing multiplication:
4x = 20
What number would work? That is right, 5.
x = 5
What would you do to 20 to get 5? Divide by 4. Holy smokes! That is the exact opposite of what the equation is doing. Here is another:
x7 = 4
What number divided by 7 equals 4? That’s it, 28. We times 4 by 7 to get that answer. Multiplying by 7 is the exact opposite of dividing by 7.
This leads us to a couple of conclusions that form the basis for everything we will do in Algebra:
1. When we want to get rid of numbers that are surrounding the variable, we need to do the opposite (technically called the inverse) of them.
|
|
|
2. We can add, subtract, multiply, or divide both sides of an equation by any number and still have the equation work.
|
Here is how it would work, one of each:
x+7=11 |
4x=24 |
x-3=24 |
x5 = 7 |
-7 -7 |
/4 /4 |
+3 +3 |
(5) (5) |
x = 4 |
x = 6 |
x = 27 |
x = 35 |
You may ask why we go through all of that when the answers are obvious. The answer is that these problems will not be so easy later on, and we need to practice these easy ones so that when we get the hard ones, they crumble before our abilities. Now to some which are a little tougher.
When we have one like this:
2x – 7 = 11
We could think about it long enough to find a number that works, and maybe you can do that, but I have to tell you that in just a little while we are going to have a problem that you won’t be able to do that with too quickly. So, let’s use what we learned to get rid of the 2 and the 7 so that x will be left by itself. If you remember the order of operations, you will remember that the 2 and the x are stuck together by multiplication, so we can’t get rid of the 2 until the 7 has been taken care of like this:
2x – 7 = 11 |
|
2x = 18 |
(we added 7 to both sides) |
x = 9 |
(divided both sides by 2) |
To illustrate the idea of un-doing operations, I would like to try to stump you with math tricks.
We begin. I am thinking of a number, and it is your job to guess what the number is.
I am thinking of a number. |
Not too hard to figure out, you say? You're right. The answer is 5 and you obtained that by taking the result and going backwards. Try the next one:
I am thinking of a number. |
Aha. A little tougher don't you think? Well, If you think about it just one step at a time, then the thing falls apart. What number would I add 4 to to get 18? 14 (notice that it is just 18 subtract 4). We can just follow up the line doing the exact opposite of what I did to my number. Here you go:
Start with 18 |
That’s it! Most of Algebra is summed up in the concept of un-doing what was done.
I am thinking of a number. |
This one is done the same way as the other one but I wanted to show you how you make that into an equation that will be useful in the rest of your math career. Instead of writing each step out, we construct an equation. We write it again but this time we will write the equation along with it:
What did I start with?
That looks like a nasty equation, but it is done in exactly the same way. We just go backwards and undo all of the things that were done to the original number. We are using the rule that we can add, subtract, multiply or divide both sides of the equation by the same thing.
I know you can do it when it is all written out, so I will show you what it looks like using the equation:
| 4x+59 - 7 = -2 | add 7 to both sides |
| 4x+59= 5 | times both sides by 9 |
| 4x + 5 = 45 | subtract 5 from both sides |
| 4x = 40 | divide both sides by 4 |
x = 10
10 is the number I started with! Go ahead and make sure by sticking it into the original problem, and you will see that we found the right number. We call that number a solution, because it is the only number that solves the equation.
Solving for a variable:
When given a formula, it is sometimes requested that you solve that formula for a specific variable. That simply means that you are to get that variable by itself.
An example:
Solve for t:
| rt = d | (Original equation of rate x time = distance) |
We are supposed to get t by itself. How do we get rid of the “r”?
Divide both sides by r. It looks like this
rt = d |
|
rtr = dr |
|
t = dr |
Done. 't' is by itself. |
Another example:
| Solve for x: | |
y = bx + c |
subtract “c” from both sides |
y - c = bx |
Divide both sides by “b”. |
(y-c)b = x |
Done. “x” is by itself. |
Applications of linear equations
“When am I ever going to use this?” “Where would this be applicable?” All the way through math, students ask questions like these. Well, to the relief of some and the dismay of others, you have now reached the point where you will be able to do some problems that have been made out of real life situations. Most commonly, these are called, “story problems.”
The four main points to remember are:
D- Data. Write down all the numbers that may be helpful. Also, note any other clues that may help you unravel the problem.
V- Variable. In all of these story problems, there is something that you don’t know, that you would like to. Pick any letter of the alphabet to represent this.
P- Plan. Story problems follow patterns. Knowing what kind of problem it is helps you write down the equation. This section of the book divided up so as to explain most of different kinds of patterns.
E- Equation. Once you know how the data and variable fit together. Write an equation of what you know. Then solve it. This turns out to be the easy part.
|
Once you have mastered the techniques in solving linear equations, then the fun begins. Linear equations are found throughout mathematics and the real world. Here is a small outline of some applications of linear equations. You will be able to solve any of these problems by the same methods that you have just mastered.
Translation
The first application is when you simply translate from English into math. For example:
Seven less than 3 times what number is 39?
3x - 7 = 39 |
then solve |
3x = 46 |
|
x = 463 |
(or 1513 or 15.3) |
That’s the number.
Substitution
Sometimes you are given a couple of different things to find. Example:
Two numbers add to 15, and the second is 7 bigger than the first. What are the two numbers?
Pick some letters to represent what you don’t know. Pick whatever is best for you. I will choose the letter “f” for the first number and “s” for the second. I then have two equations to work with:
f + s = 15 and s = f + 7 |
The letter “s” and “f + 7” are exactly the same and can be changed places. |
f + f + 7 = 15 |
|
2f + 7 = 15 |
|
2f = 8 |
|
f = 4 |
4 must be the first number, but we need to stick it back in to one of the original equations to find out what “s” is.
s = f + 7 |
|
= 4 + 7 |
|
= 11 |
4 and 11 are our two numbers. |
These kinds of problems often take the form of an object being cut into two pieces. Here, I will show you what I mean.
Example:
A man cuts a 65 inch board so that one piece is four times bigger than the other. What are the lengths of the two pieces?
Now, I would personally pick “f” for first and “s” for second. We know that
f + s = 65 and that s = 4f
thus,
f + 4f = 65 |
Shapes
With many of the problems that you will have, pictures and shapes will play a very important role. When you encounter problems that use rectangles, triangles, circles, or any other shape, I would suggest a few things:
- Read the problem.
- READ the problem again.
- READ THE PROBLEM one more time.
Once you draw a picture to model the problem, read the problem again to make sure that your picture fits.
The formulas for the shapes that we will be discussing are found in Section 2.2.
Variable on Both Sides
Unfortunately, not all equations come out such that this un-doing technique works. Sometimes the x shows up in several different places at once:
3x – 5 +2x – 3 = 5x + 7(x – 8)
Seeing all of the x’s scattered throughout the equation sometimes looks daunting, but it isn’t as bad as all that. We know a couple of ways to make it look a bit more simple.
3x - 5 + 2x - 3 |
= |
4x + 7(x - 8) |
Distribute the 7 and combine |
5x - 8 |
= |
4x + 7x - 56 |
Combine the like terms |
5x - 8 |
= |
11x - 56 |
Final result |
| Now we reach a point where you should feel somewhat powerful. Remember that you can add, subtract, multiply, or divide anything you want! (As long as you do it to both sides.) |
|
|
| Particularly, I don’t like the way that 11x is on the left hand side. I choose to get rid of it! So, I subtract 11x from both sides of the equation: | ||
5x – 8 = 11x – 56 |
||
-11x -11x
Upon combining the like terms, I get -6x - 8 = -56 Which now is able to be un-done easily: -6x = -48 (add 8 to both sides) |
Special Cases:
What about 2x + 1 = 2x + 1
Well if we want to get the x’s together we had better get rid of the 2x on one side. So we subtract 2x from both sides like this:
2x + 1 = 2x + 1
-2x -2x
1 = 1
Ahh! The x’s all vanished
|
Well, what do you think about that? This statement is always true no matter what x is. That is the point. x can be any number it wants to be and the statement will be true. All numbers are solutions. |
|
|
On the other hand try to solve: 2x + 1 = 2x + 5 |
|
Again, the x’s all vanished. This time it left an equation that is never true. No matter what x we stick in, we will never get 1 to equal -5. It simply will never work. No solution. |
||
Section 3.1 Exercises
Part A
Section 3.1 Exercises Part APart B
Section 3.1 Exercises Part BPart C
Section 3.1 Exercises Part C
Section 3.2
Percents
If you scored 18 out of 25 points on a test, how well did you do? Simple division tells us that you got 72%. As a review, 1825 = .72
If we break up the word “percent” we get “per” which means divide and “cent” which means 100. Notice that .72 is really the fraction 72100.
We see that when we write it as a percent instead of its numerical value, we move the decimal 2 places. Here are some more examples to make sure that we get percents:
.73 = 73%
.20 = 20%
.05 = 05%
1 = 100%
2.3 = 230%
The next reminder, before we start doing problems, is that the word “of” often means “times.” It will be especially true as we do examples like:
What is 52% of 1358?
All we need to do is multiply (.52)(1358) which is 706.16.
Sometimes however, it isn’t quite that easy to see what needs to be done. Here are three examples that look similar but are done very differently. Remember, “what” means “x”, “is” means “=” and “of” means times.
| What is 15% of 243? x = .15(243) x = 36.45 |
15 is what percent of 243? 15 = x(243) .062 = x 6.2% = x |
15 is 243% of what? 15 = 2.43x 6.17 = x |
Once we have that down, we have the ability to solve tons of problems involving sales tax, mark-ups, and discounts. Here are two examples:
An item sells for $85.59 but is on sale at 20% off. What is the final price? |
An item sold at $530 has already been marked up 20%. What was the price before the mark-up? |
|
.2(85.59) = 17.12 |
amount of discount |
x + .2x = 530 (original + 20% of original = final price) |
85.59 - 17.12 |
subtract discount |
1.2x = 530 x = 441.67 |
| $68.47 = final price | ||
Equations with Fractions
The one other thing that might throw you off is when you see a bunch of fractions in the problem. Not to worry, remember that you have power to do anything you want to the equation.
For example:3x8 - 58 = 7x8 might be easier to look at if there weren’t so many fractions in the way. Well, get rid of them. Multiply by 8 on both sides.
(8)*3x8 - (8)*5x8 = (8)*7x8 which makes it become:
3x - 5 = 7x (not bad at all)
-5 = 4x
-54 = x (Ta da.)
Worse example:
27 - x-34 = 5 looks scary.
You have the ability to wipe out all of the fractions. Fractions are simply statements of division. The opposite of division is multiplication – and you have the power to multiply both sides of the equation by anything you want to. The question is, what will undo a division by 7 and by 4; the answer is multiplication by 28. Here is what it looks like:
| 1. Simplify | 27 - x-34 = 5 | ||
| (28)27 - (28)x-34 = (28)5 | Multiplying everything by 28 | ||
| (4)2 - (7)(x-3) = 140 | (287 = 4 and 284 = 7 ) | ||
| 8 - 7x + 21 = 140 | (Distribute the -7) | ||
| -7x +29 = 140 | (Combine numbers) | ||
| 2. Subtract | -7x = 111 | (Subtract 29 from both sides) | |
| 3. Divide | x = -1117 | (Not a nice looking answer, but it is right!) |
Every problem can be boiled down to three steps:

Section 3.2 Exercises
Part A
Section 3.2 Exercises Part APart B
Section 3.2 Exercises Part BPart C
Section 3.2 Exercises Part C
Section 3.3
The rules that come with exponents are relatively easy to understand, but they take some practice to ensure that you have them down completely. Instead of numbers we will use letters. If we multiply:
x5x8
We just have to remember what that means:
(xxxxx)(xxxxxxxx),
which is simply 13 of them multiplied together.
We write it as x13.This is our very first rule! Exponents add during multiplication.
x5x8 = x13
The next one is quite similar:
(x5)8
Again, we just have to remember what it means:
(x5)(x5)(x5)(x5)(x5)(x5)(x5)(x5)
Which is by the first rule: x40
That gives us the second rule: Exponent to exponent will multiply.
(x5)8 = x40
Division with exponents is just about as easy. Looking at:
x8x5
This means: (xxxxxxxx)(xxxxx) and we are left with x3.
Third rule: Exponents subtract during division.
This particular rule gives rise to a couple of interesting facts. Specifically, what happens if the top and the bottom have the same power?
x8x8 = x0
But, we know that anything divided by itself is equal to 1. Thus:
x0 = 1
Secondly, what happens if the number on the bottom is larger than the one on the top.
For example:
x5x8
By using the third rule we get
x5x8 = x5 - 8 = x -3,
a negative exponent! What do we do with that? Well, if we do it the long way, we get:
xxxxxxxxxxxxx. which is: 1x3
Thus we have our next definition. A negative exponent puts the number on the bottom.
x-3 = 1x3
Let’s look at a couple of examples:
| Using rules of exponents | Checking with numbers | |
| 23 * 22 = 25 = 2 * 2 * 2 * 2 * 2 = 32 | 23 * 22 = 8 * 4 = 32 | |
| 2724 = 27 - 4 = 23 = 8 | 2724 = 12816 = 8 |
Look at that. The rules really work for any number. Here are some more examples to be able to simplify some expressions:
(3x5)3 = 27x15 by use of the second rule.
(4y5)(7y12) = 28y17 by use of the first rule.
2-6 = 126 = 164
6-2 = 162 = 136
17-2 = 1149 = 49
(3x1115x4)-2 = (x115x4)-2 = (x75)-2 = (x-145-2) = 52x14 = 25x14
Here is a summary of how you can simplify expressions with exponents:
Rule |
Official | Example | Why |
|---|---|---|---|
Multiplication: add exponents |
aman = am + n |
3x2 * 2x5 = 6x7 |
3xx2xxxxx = 6xxxxxxx = 6x7 |
Exponent to a power: multiply exponents |
(am)n = amn |
(5x2)3 = 125x6 |
(5x2)(5x2)(5x2) = 125x6 |
Division: subtract exponents |
aman = am - n |
36x84x6 |
36xxxxxxxx4xxxxxx = 9xx = 9x2 |
Exponent of 0 |
a0 = 1 if a ≠ 0 |
70 = 1; x0 = 1 |
1 = x7x7 = x0 by division rule |
Negative exponent |
a-n = 1an |
2-4 = 124 = 116; 1x-7 = x7 |
1x5 = xxxxxxxxx = x2x7 = x-5 |
Compounding Quarterly, Monthly, and Daily
So far, you have been compounding interest annually, which means the interest is added once per year. However, you will want to add the interest quarterly, monthly, or daily in some cases. Excel will allow you to make these calculations by adjusting the interest rate and the number of periods to be compounded. Remember that all interest rates provided in the problems are annual rates.You must adjust them to fit other compounding periods. The adjusted rate is called the periodic rate. To adjust the periodic rate in Excel, open the FV calculation box and change a 10% annual rate to quarterly, monthly, or daily as follows:
Quarterly |
Rate: | .104 | Changing the rate to 2.5% or .025 |
Monthly |
Rate: | .1012 | Changing the rate to .83% or .0083 |
Daily |
Rate: | .10365 | Changing the rate to .0274% or .000274 |
Change ten years of compounding to quarterly, monthly, or daily as follows:
Quarterly |
Nper: | 10 * 4 | Changing the compounding periods to 40 |
Monthly |
Nper: | 10 * 12 | Changing the compounding periods to 120 |
Daily |
Nper: | 10 * 365 | Changing the compounding periods to 3,650 |
Assume you put $50 into savings and you are comparing savings accounts where the 10% annual interest rate is compounding quarterly, monthly, or daily. You can compare the amount of interest you will earn using Excel as follows:
| Quarterly | Monthly | Daily |
|---|---|---|
Rate: .14 or .025 |
Rate: .112 or .008333 |
Rate: .1365 or .000274 |
Nper: 10 * 4 or 40 |
Nper: 10 * 12 or 120 |
Nper: 10 * 365 or 3650 |
Pmt: 0 |
Pmt: 0 |
Pmt: 0 |
Pv: -50 |
Pv: -50 |
Pv: -50 |
Future Value: $134.25 |
Future Value: $135.35 |
Future Value: $135.90 |
The more frequently interest is added to your savings and compounded, the more interest you will earn. The above illustration involves a small amount of savings. The more the savings and the more often you add to your savings the more difference it will make when the interest is added and compounded more frequently. The following example illustrates saving $100 per month for ten years at 10% interest rate compounded monthly versus annually.
| Annually | Monthly |
|---|---|
Rate: .1 or 10% |
Rate: .112 or .008333 |
Nper: 10 |
Nper: 10 * 12 |
Pmt: -1200 |
Pmt: -100 |
Pv: 0 |
Pv: 0 |
Future Value: $19,124.91 |
Future Value: $20,484.50 |
Savings Plan Formula for a lump sum
|
A = Final amount So, nY = number of periods (nper) |
|||||
Savings Plan Formula with payment
|
||||||
Thus we have the monster formula for a Savings Plan that begins with a balance and then is added to by a payment:
|
Spreadsheets normally have this formula built into their functions. It is known as Future Value (FV), so you won’t need to use this one if you learn the spreadsheet well.
Loan Payment Formula
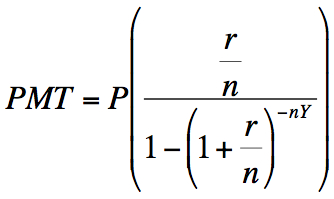
Spreadsheets also normally have this formula built into their functions. It is known as Payment (PMT).
Final note using a spreadsheet: The formulas are built so that money going out from you is negative and money coming in to you is positive. When you are entering Savings into the spreadsheet, the payment and Principal (Present Value) will be negative. However, for a loan, the payment will be negative but the Principal (Present Value) will be positive, because it represents money coming to you.
Calculating Payments, Interest Rates, and Number of Periods
Excel will help you calculate the payment you will need to make on a loan. It will calculate the interest rate you would need to earn on your savings to realize a certain future balance. The number of periods it will take to have your savings grow to a certain future balance can also be determined.
Monthly Payment Calculation If you wanted to buy a car that costs $15,000 and you can get a loan at 6% interest for four years, you can determine the monthly payments using the PMT Excel function as follows: |
||
Rate: .06/12 or .005 (monthly interest) Nper: 4*12 or 48 (months) Pv: -15000 Fv: 0 Monthly Payment = $352.28 |
||
When you have paid the monthly payment for forty-eight months you will own the car, and the future value of the loan is zero because the loan in paid off. |
||
Benefits Versus Bondage
You can see how hard your savings will work for you given an interest rate and enough time. However, interest works against you when you borrow money. The benefits may seem great at the moment but the financial bondage is terrible. By calculating the interest you would pay on a loan to borrow a car and the interest you would earn by saving to pay cash for the car, we can determine the financial advantage of collecting interest rather than paying interest.
Interest Paid on a Car Loan You calculate the amount of interest you would pay on a four year car loan of $15,000 at 6% annual interest using the Excel Pmt function as follows: |
||
Rate: .06/12 Section 3.3 Total Payment = $352.28*48 (Payments) = $16,909.22 Interest Paid =$16,909.22 (Paid) -$15,000 (Borrowed) = $1,909.22 |
||
TIP: You can have Excel calculate this for you by entering the Pmt function to calculate the monthly payment and then, on the formula bar at the top of the Excel sheet, multiply by 48 payments and subtract the $15,000 you borrowed. The formula will be as follows: =PMT(0.06/12,4*12,-15000,0)*48-15000 |
||
You can also double click on the cell with the Pmt calculation in it and the formula will appear in the cell. Now you can multiply by 48 payments, subtract 15000, and enter this formula in the cell. The cell will have the answer and the formula will be in the formula bar.
Interest Collected on Your SavingsThe interest you will earn on your savings of $350.00 per month earning 6% annual interest for 39 months (the number of months we calculated above would be required to accumulate $15,000 in savings) is calculated using the FV function in Excel as follows:
| Rate: .06/12 Nper: 39 Pmt: -350 Pv: 0 FV = $15,030.44 Amount Deposited in Savings = $350*39 (deposits) = $13,650.00 Interest Earned on Savings = $15,030.44-$13,650.00 = $1,380.44 |
Again, you can double click on the cell containing the FV calculation and subtract 350 * 39 and enter this formula giving you the amount of interest earned. You can make the same adjustment to the formula in the formula bar. The resulting formula is as follows:
=FV(0.06/12,39,-350)-350*39
Total Savings from Saving Versus Borrowing
Here is how you benefited by saving and paying cash for the car rather than borrowing the money:
Interest Earned |
$1,380.44 |
Interest Not Paid |
$1,909.22 |
Financial Advantage |
$3,289.66 |
You are wealthier by $3,289.66 because you collected interest rather than paying interest. This practice will make a major difference in your financial wellbeing throughout your life. If you put the money you save by paying cash for major purchases to work for you by investing it for your retirement, you will add greatly to your independent wealth. You can estimate that using the FV function in Excel as follows, assuming a 6% return on your investment for 30 years:
Rate: .06 |
This addition to your wealth along with the other additions resulting from saving rather than borrowing will make a major impact on your ultimate wealth.
TIP: In all of the Excel functions you will be using, you only need three entries or factors to calculate the fourth factor you are after. Notice that there are only three entries in each of the above Excel functions. You can leave blank any factor not needed and Excel will assume it is zero.
Section 3.3 Exercises
Part A
Section 3.3 Exercises Part APart B
Section 3.3 Exercises Part BPart C
Section 3.3 Exercises Part C

