Chapter 1: Arithmetic
Section 1.1: Facts
Everyone has to start somewhere, and that start, for you, is right here. When you first started learning math, you probably learned the names for numbers and then you started to add: 3 apples + 7 apples equals how many apples? Well 10, of course.
My guess is that you caught on to what you were doing and can now add m&ms, coconuts, gallons of water, money, etc. From the beginning I am going to assume you know how to add in your head up to 15+15. If you don't, please make up some flash cards and get those in your brain. It is similar to learning the alphabet before learning to read. We need the addition facts to be available for instant recall.
Soon after addition was learned, I bet someone told you that there was a shortcut when you had to add some numbers up over and over. For example:
3+3+3+3+3+3+3(Seven 3s) = 21
If you notice, there are seven 3s. 3, seven times, turns out to be 21, so we write it as 7x3 = 21.
One of the best coincidences of the world is that 7, three times, is also 21.
3x7 = 21
Such a switching works for any numbers we pick:
4x5 = 20 and 5x4 = 20
3x13 = 39 and 13x3 = 39
Since we will be using the multiplication facts almost as much as we will be using the addition facts, you need to also memorize the multiplication facts up to 15x15. Learn them well, and you will be able to catch on to everything else quite nicely.
Section 1.1 Exercises
Part A
- Make flash cards up to 15+15 and 15x15.
- Memorize the addition and multiplication facts up to 15+15 and 15x15.
- Fill out Addition/Subtraction Monster. Time yourself. Write the time it takes on the paper.
- Fill out Multiplication Monster. Time yourself. Write the time on the paper.
To view the following files, right click and select save link as, or just view in your browser.
Section 1.1 Exercises Part APart B
Section 1.1 Exercises Part BPart C
Section 1.1 Exercises Part C
Section 1.2: Rounding and Estimation
Now, you know that some arithmetic problems may get long and tedious, so you can understand why some folks choose to estimate and round numbers. Rounding is the quickest, so we will tackle that first.
In rounding, we decide to not keep the exact number that someone gave us. For example:
Rounding
If I have $528.37 in the bank, I might easily say that I have about $500. I have just rounded to the nearest hundred.
On the other hand, I might be a little more specific and say that I have about (still not exact) $530. I have just rounded to the nearest ten.
Here are the places:
Just to make sure you are clear on it, here is a big example:
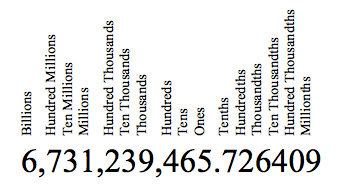
Example
Round to the nearest hundredth:
538.4691
This number is right between 538.46 and 538.47
Which one is nearest? The 9 tells us that we are closer to
538.47
2nd Example:
Round to the nearest thousand:
783,299.4321
This number is right between 783,000 and 784,000
Which one is nearest? The 2 in the hundreds tells us that we are closer to:
783,000
Last Example
Round $4,278.23 to the nearest hundred
| $4,278.23 =>$4,300.00$4,200.00 | Decide if our number is closer to the nearest hundred above the number or below the number |
| $4278.23 ≈ $4,300.00 | Change our number to the one it is closer to |
Answer: $4,300.00
Estimation
Estimation
|
Once rounding is understood, it can be used as a great tool to make sure that we have not missed something major in our computations. If we have a problem like:
3,427,000
x 87.3
We could see about where the answer is if we estimate first:
Round each number to the greatest value you can
3,000,000
x 90
Voila! Our answer will be around 270,000,000
We should note that the real answer is:
299,177,100
but the estimation will let us know that we are in the right ball park. It ensures that our answer makes sense.
Estimation
|
Last Example
Multiply by rounding: 986.7×4.9
| 986.7 ≈ 1,000 4.9 ≈ 5 |
Round the numbers |
| 1,000 x 5 = 5,000 | Multiply the rounded numbers together |
| 986.7 x 4.9 ≈ 5,000 | Our answer for 986.7 x 4.9 will be around 5,000 |
Section 1.2 Exercises
To view the following files, right click and select save link as, or just view in your browser.
Part A
Section 1.2 Exercises Part APart B
Section 1.2 Exercises Part BPart C
Section 1.2 Exercises Part C
Section 1.3: Decimals
Definitions & Basics
- Like Things- In addition and subtraction we must only deal with like things.
- Example: If someone asks you
5 sheep + 2 sheep = you would be able to tell them 7 sheep. - What if they asked you 5 sheep + 2 penguins = We really can’t add them together, because they aren’t like things.
- We do not need like things for multiplication and division.
- Negative- The negative sign means “opposite direction.”
- Example: -5.3 is just 5.3 in the opposite direction {Graph of 5 and -5}
- Example: -78 is just 78 in the opposite direction.
- Example: : -7 – 5 = -12, because they are both headed in that direction
- Decimal- Deci is a prefix meaning 10. Since every place value is either 10 times larger or smaller than the place next to it, we call each place a decimal place.
- Place Values- Every place on the left or right of the decimal holds a certain value
Arithmetic of Decimals, Positives and Negatives
LAWS & PROCESSES
Addition of Decimals
|
EXAMPLE
| Add 3561.5 + 274.38 | |
|---|---|
| 3561.5 + 274.38 |
1. Line up decimals |
| 3561.5 + 274.38 5.88 |
2. Add in columns |
| 1 3561.5 + 274.38 3835.88 |
3. Carry by 10's. Carry the 1 and leave the 3. |
Subtraction of Decimals
|
EXAMPLE
| Subtract 283.5 - 3,476.91 | |
|---|---|
| -3476.91 283.5 |
1. Biggest on top |
| -3476.91 283.5 |
2. Line up decimals; subtract in columns |
| 3 -3 4 17 6 . 9 1 2 8 3 . 5 3 1 9 3 . 4 1 |
3. Carry by 10's. Carry the 1 and leave the 3. |
| 3 -3 4 17 6 . 9 1 2 8 3 . 5 -3 1 9 3 . 4 1 |
3. Biggest one wins |
Multiplication of Decimals
Multiplication of Decimals
|
EXAMPLES
29,742
x 538
| Start: 29,742 x 538 |
29,742 x 8237,936 |
| Next: 29,742 x 538237,936 |
29,742 x 30892,260 |
| Last: 29,742 x 538237,936 892,260 |
29,742 x 50014,871,000 |
| Then: 29,742 x 538 237,936 892,260 +14,871,000 |
Add the pieces together |
Final answer:
16001196
Final example with decimals:
-7414.3
x 9.46
| Start: -7414.3 x 9.46 |
-7414.3 x 6444858 |
| Next: -7414.3 x 9.46444858 |
-7414.3 x 402965720 |
| Last: -7414.3 x 9.46444858 2965720 |
-7414.3 x 90066728700 |
| Then: -7414.3 x 9.46 444858 2965720 +66728700 |
1. Add the pieces together 2. Make it the right size: Number of decimal places = 3 Answer is negative |
The only thing left is to count the number of decimal places. We have one in the first number and two in the second. Final answer:
-70139.278
Division of Decimals
Division of Decimals
|
EXAMPLES
429÷8
 |
Step 2. We know that 8 goes into 42 about 5 times. |
 |
Step 3. Multiply 5x8 Step 4. Subtract |
 |
Step 5. Bring down the 9 to continue on. Repeat 2-5 Step 2. 8 goes into 29 about 3 times. |
 |
Step 3. Multiply 3x8 Step 4. Subtract |
| 8 doesn't go into 5 (remainder) |
Which means that 429÷8 = 53 R 5 or in other words 429÷8 = 53 58
Example 2: 5875÷22
 |
Step 2. We know that 22 goes into 58 about 2 times. Step 3. Multiply 2x22 = 44 |
 |
Step 4. Subtract Step 5. Bring down the next column |
 |
22 goes into 147 about ???? times. Let's estimate. 2 goes into 14 about 7 times. - try that Multiply 22x7 = 154 Oops, a little too big |
 |
Since 7 was a little too big, try 6 Multiply 6x22 = 132 Subtract Bring down the next column. |
 |
22 goes into 155 about ???? times. Estimate. 2 goes into 15 about 7 times. Try 7 Multiply 22x7 = 154 It worked. Subtract Remainder 1 |
5875÷22 = 267 R 1 or in other words 5875÷22 = 267 122
An example resulting in a decimal: Write 49 as a decimal
 |
Step 1: Set it up. Write a few zeros, just to be safe. |
 |
Step 2: Divide into first. 9 goes into 40 about 4 times. Step 3. Multiply 4x9 = 36 Step 4. Subtract |
 |
Step 5. Bring down the next column. Repeat steps 2-4 Step 2: 9 goes into 40 about 4 times. Step 3. Multiply 4x9 = 36 Step 4. Subtract |
 |
Step 5. Bring down the next column. Repeat steps 2-4 Step 2: 9 goes into 40 about 4 times. Step 3. Multiply 4x9 = 36 Step 4. Subtract This could go on forever! |
Repeating decimal: Thus 49 = .4444... which we simply write as .4
The bar signifies numbers or patterns that repeat
Two final examples:
| 358.4÷ -(.005) | 296÷3.1 | |
 |
Step 1. Set it up and move the decimals |  |
 |
Step 2. Divide into first Step 3. Multiply down |
 |
 |
Step 4. Subtract Step 5. Bring down the next column. |
 |
 |
Repeat steps 2-4 as necessary Step 2. Divide into first Step 3. Multiply down Step 4. Subtract Step 5. Bring down the next column. |
 |
 |
Repeat steps 2-4 as necessary Step 2. Divide into first Step 3. Multiply down Step 4. Subtract Step 5. Bring down the next column. |
 |
 |
Repeat steps 2-4 as necessary Step 2. Divide into first Step 3. Multiply down Step 4. Subtract Step 5. Bring down the next column. |
 |
 |
Repeat steps 2-4 as necessary Step 2. Divide into first Step 3. Multiply down Step 4. Subtract Step 5. Bring down the next column. |
 |
| -71680 | Step 6. Write answer | 95.483... |
COMMON MISTAKES
Two negatives make a positive
- True in Multiplication and Division– Since a negative sign simply means other direction, when we switch direction twice, we are headed back the way we started.
Example: -(-5) = 5
Example: -(-2)(-1)(-3)(-5) = - - - - -30 = -30
Example: -(-40 ÷ -8) = -(- -5) = -5
- False in Addition and Subtraction– With addition and subtraction negatives and positives work against each other in a sort of tug o’ war. Whichever one is stronger will win.
Example: Debt is negative and income is positive. If there is more debt than income, then the net result is debt. If we are $77 in debt and get income of $66 then we have a net debt of $11:
-77 + 66 = -11
On the other hand if we have $77 dollars of income and $66 of debt, then the net is a positive $11:
77 – 66 = 11
Example: Falling is negative and rising is positive. An airplane rises 307 feet and then falls 23 feet, then the result is a rise of 284 feet:
307 – 23 = 284
If, however, the airplane falls 307 feet and then rises 23 feet, then the result is a fall of 284 feet:
-307 + 23 = -284
Other examples: Discount it negative and markup or sales tax is positive. Warmer is positive and colder is negative. Whichever is greater will give you the sign of the net result.
Percent: Percent can be broken up into two words: “per” and “cent” meaning per hundred, or in other words, hundredths.
Example: 7100 = .07 = 7% 31100 = .31 = 31% 53100 = .53 = 53%
Notice the shortcut from decimal to percents: move the decimal right two places.
LAWS & PROCESSES
Converting Percents
Percents
|
EXAMPLE
Convert .25 to a percent
| .25 = 25% | Move the decimal two places to the right because we are turning this into a percent |
.25 = 25%
What is 532 as a percent?
| 5÷32 = .15625 | Turn the fraction into a percent |
| .15625 = 15.625% | Move the decimal two places to the right because we are turning this into a percent |
532 = 15.625%
Convert 124% to decimals
| 124% = 1.24 | Move the decimal two places to the left because we are turning this into a decimal |
124% = 1.24
Solving “Of” with Percents
The most important thing that you should know about percents is that they never stand alone. If I were to call out that I owned 35%, the immediate response is, “35% of what?” Percents always are a percent of something. For example, sales tax is about 6% or 7% of your purchase. Since this is so common, we need to know how to figure this. If you buy $25 worth of food and the sales tax is 7%, then the actual tax is 7% of $25.
| Percents In math terms the word “of” means times. |
.07x25 = $1.75
What is 25% of 64
| 25% = .25 | Turn percent into a decimal |
| .25 x 64 = 16 | Multiply the two numbers together |
25% of 64 is 16
What is 13% of $25
| 13% = .13 | Turn percent into a decimal |
| .13 x 25 = 3.25 | Multiply the two numbers together |
13% of $25 is $3.25
What is 30% of 90 feet
| 30% = .30 | Turn percent into a decimal |
| .30 x 90 = 27 | Multiply the two numbers together |
30% of 90 feet is 27 feet
Section 1.3 Exercises
Part A
Section 1.3 Exercises Part APart B
Section 1.3 Exercises Part BPart C
Section 1.3 Exercises Part C
Section 1.4 Arithmetic of Fractions, Positives, and Negatives
DEFINITIONS & BASICS
- Numerator – the top of a fraction
- Denominator – the bottom of the fraction
- Simplify – Fractions are simplified when the numerator and denominator have no factors in common.
- One – any number over itself = 1.
- Common Denominators – Addition and subtraction require like things. In the case of fractions, “like things” means common denominators.
- Prime Factorization – Breaking a number into smaller and smaller factors until it can not be broken down further.
LAWS & PROCESSES
Prime Factorization – One of the ways to get the Least Common Denominator for fractions that have large denominators is to crack them open and see what they are made of. Scientists get to use a scalpel or microscope. People in math use prime factorization.
Addition of Fractions
|
EXAMPLE
Add 34 + 12
| 34 + 12 -> 24 | The least common multiple of 4 and 2 is a 4, so we replace the 1/2 with another form, which is 2/4 |
| 34 + 24 = 5 | Now that the denominators are the same, add the numerators. |
| 34 + 24 = 54 | Carry the denominator across. |
34 + 12 = 54
Changing from mixed numbers to improper fractions:
5 38 = 5 + 38 = 408 + 38 = 438
Changing them back again:
374 = 37÷4 = 9 R 1 = 9 14
Subtraction of Fractions
|
EXAMPLE
Do this: 59 - 3 13
| - | 3 13 is bigger, so put it on top |
| - | The common denominator is 9, so change to a 13 to a 39 |
| -59 = - | Subtract the numerators borrow by denominator as needed |
59 - 3 13 = -2 79
Multiplication of Fractions
|
EXAMPLE
| 56 x 13 | For multiplication don't worry about getting common denominators |
| 56 x 13 = 5 | Multiply the numerators straight across |
| 56 x 13 = 518 | Multiply the denominators straight across |
56 x 13 = 518
Divison of Fractions
|
EXAMPLE
Divide 347 ÷ 23
| 3x77 + 47 ÷ 23 -> 257 ÷ 23 | Turn the fractions into improper fractions |
| 257 x 32 | Keep the first fraction the same. Change the division sign to a multiplication sign. Flip the second fraction’s numerator and denominator |
| 257 x 32 = 7514 | Multiply straight across the numerator and denominator |
347 ÷ 23 = 7514
1Divide 25 ÷ 134
| 25÷1x44 + 34 -> 25÷74 | Turn the fractions into improper fractions |
| 25 x 47 | Keep the first fraction the same. Change the division sign to a multiplication sign. Flip the second fraction’s numerator and denominator |
| 25 x 47 = 835 | Multiply straight across the numerator and denominator |
25 ÷ 134 = 835
Now that you have had a little time to multiply fractions together and simplify them. You may have noticed one of the slickest tricks that we can do with fractions, and that is that we can actually do the simplification before we multiply them. Take for example:
1063 x 2155
Now, we can do this the normal way or we can try to see if there is anything that we will be simplifying out later . . . and do that simplification before we multiply:
Normal method:
1063 x 2155 = 2103465
and now we try to simplify
2103465 = 2x3x5x73x3x5x7x11
which probably took quite a while to get. So,
2103465 = 2x3x5x73x3x5x7x11 = 23x11 = 233
New and improved slick method:
1063 x 2155 =
and we try to see if anything will cancel ahead of time
|
2x |
| |
| 1063 x | 2155 = | 233 |
|
3x |
|
What I was hoping to show is that the same answer was obtained and the same cancelling was done, but if you are able to see it before you multiply, then you will be able to simplify in a much simpler way. Here is another example:
411 x 58
the 4 and the 8 can simplify before we multiply:
-4-11 x 5-8-2 = 522
This may seem like just a convenient way to make the problem go a bit quicker, but it does much more than that. It opens the door to a much larger world. Here is an example. If we travelled 180 miles on 12 gallons of gas, then we calculate the mileage by 180 miles/12 gallons = 15 miles per gallon.
Carrying that example just a bit further, what if gas were $3.2 per gallon? We can actually find how many miles we can drive for one dollar:
180 miles12 gallons × 1 gallon3.2 dollars = 4.7 miles per dollar.
Another Example
Carpet is on sale for 15 dollars per square yard. How much is that in dollars per square foot (9 ft2 per yd2)?
Now, knowing that we will be able to cancel anything on the top with anything that is the same on the bottom, we write the multiplication so the the yd2 will cancel out, leaving us with dollars per ft2:
15 dollars1 yd2 × 1 yd29 ft2
Then cancel the yd2:
15 dollars1 yd2 × 1 yd29 ft2 = 53 dollars per square foot = $1.67 per square foot 
One more example:
A rope costs $15 for 8 feet. How much does is cost per inch? We want to get rid of feet and get inches, so we write the multiplication: 185dollars8 feet x 1 foot124 inches = 5 dollars32 inches = $.156 or 15.6 cents per inch

Here are a few numbers that will help you with the conversions:
- 12 in = 1 foot
- 16 oz = 1 pound
- 60 seconds = 1 minute
- 1000 watts = 1 kilowatt
- 1 yd = 3 ft
- 60 minutes = 1 hour
- 1 yd2 = 9 ft2
And also some exchange rates with the American dollar as they were sometime in 2010:
- 1 Mexican Peso = $0.08
- 1 Euro = $1.30
- 1 British Pound = $1.50
- 1 Brazillian Real = $0.55
Section 1.4 Exercises
Part A
Section Exercises 1.4 Part APart B
Section Exercises 1.4 Part BPart C
Section Exercises 1.4 Part C